題目描述

上課的時候總會有一些同學和前後左右的人交頭接耳，這是令小學班主任十分頭疼的一件事情。不過，班主任小雪發現了一些有趣的現象，當同學們的座次確定下來之後，只有有限的D對同學上課時會交頭接耳。

同學們在教室中坐成了 M 行 N 列，坐在第i行第j列的同學的位置是 (i,j) ，為了方便同學們進出，在教室中設定了 K 條橫向的通道， L 條縱向的通道。

於是，聰明的小雪想到了一個辦法，或許可以減少上課時學生交頭接耳的問題：她打算重新擺放桌椅，改變同學們桌椅間通道的位置，因為如果一條通道隔開了 2個會交頭接耳的同學，那麼他們就不會交頭接耳了。

請你幫忙給小雪編寫一個程式，給出最好的通道劃分方案。在該方案下，上課時交頭接耳的學生的對數最少。

輸入輸出格式

輸入格式：

輸入檔案seat.in的第一行，有5個用空格隔開的整數，分別是M，N，K，L，D（2<=N，M<=1000，0<=K<M，0<=L<N，D<=2000）。

接下來的D行，每行有4個用空格隔開的整數。第i行的4個整數Xi，Yi，Pi，Qi，表示坐在位置(Xi，Yi)與(Pi，Qi)的兩個同學會交頭接耳（輸入保證他們前後相鄰或者左右相鄰）。

輸入資料保證最優方案的唯一性。

輸出檔案seat.out共兩行。

第一行包含K個整數，a1，a2……aK，表示第a1行和a1+1行之間、第a2行和a2+1行之間、…、第aK行和第aK+1行之間要開闢通道，其中ai< ai+1，每兩個整數之間用空格隔開（行尾沒有空格）。

第二行包含L個整數，b1，b2……bL，表示第b1列和b1+1列之間、第b2列和b2+1列之間、…、第bL列和第bL+1列之間要開闢通道，其中bi< bi+1，每兩個整數之間用空格隔開（列尾沒有空格）。

輸入輸出樣例

輸入樣例#1

4 5 1 2 3
4 2 4 3
2 3 3 3
2 5 2 4

輸出樣例#1

2
2 4

說明

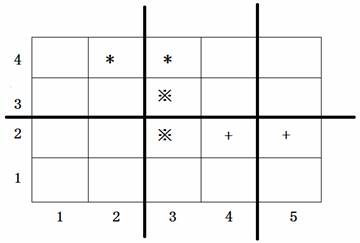
上圖中用符號*、※、+標出了 3 對會交頭接耳的學生的位置，圖中 3 條粗線的位置表示通道，圖示的通道劃分方案是唯一的最佳方案。

2008年普及組第二題

思路

題目裡提到了最優解，那麼肯定貪心做最方便了。然後從題目給的樣例解釋可以看到：如果相鄰的兩行有許多組說話的同學，那麼在這兩行中間加一條過道是非常划算的；同理，列也是如此。

只要找出劃分哪些相鄰的兩行和相鄰的兩列可以隔開的同學最多，這就是最優解了。

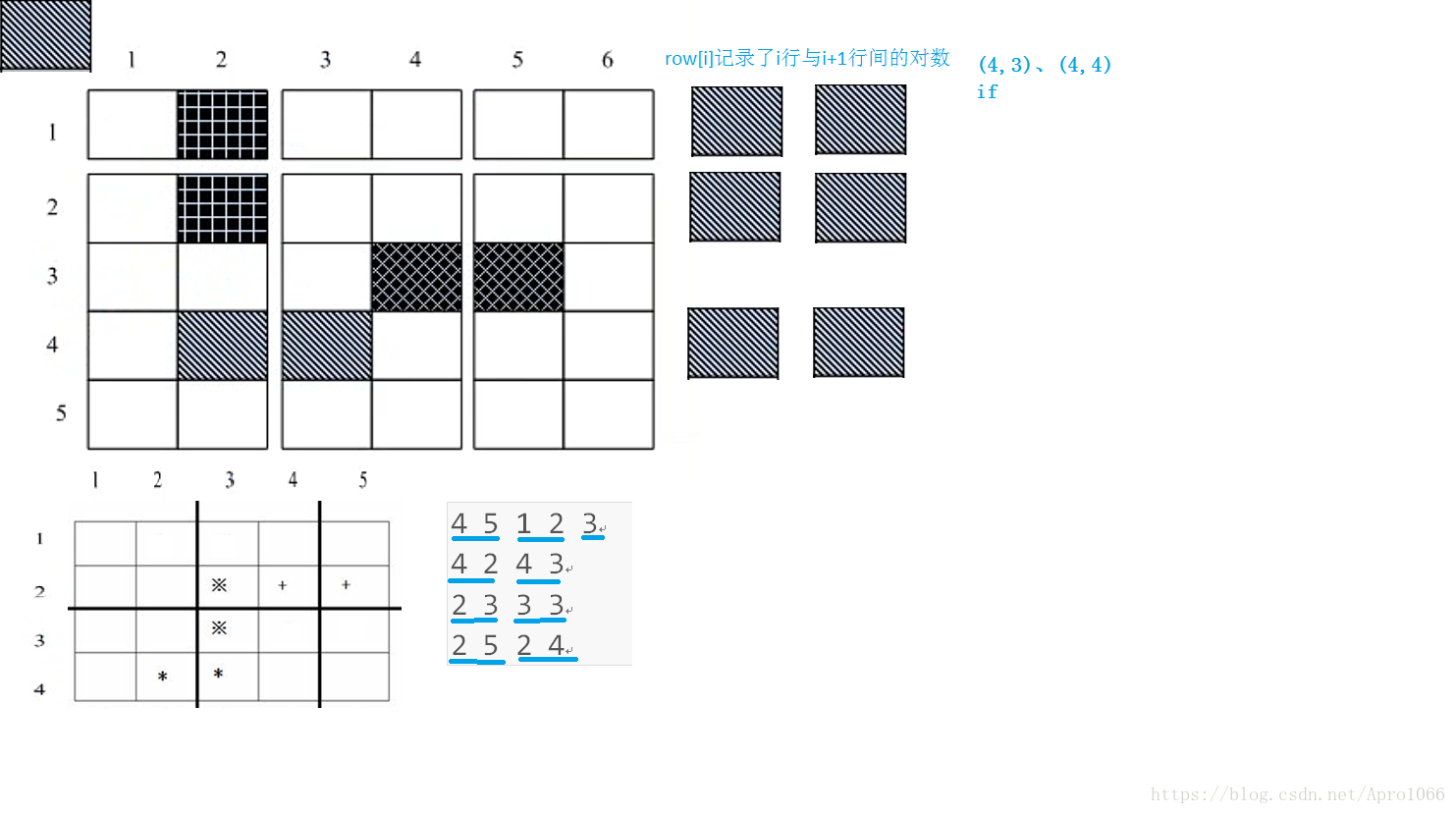
輸入兩個同學的座標，如果橫座標相同，即這兩個同學在一行，那麼設兩個同學縱座標分別為a,b 如果a<b 那麼x[a]++ 否則x[b]++（這裡一定要特判一下a和b的大小） 同理 y陣列也如此操作即可。這裡可以看成價值問題，取價值最高的畫法即可。

#include <stdio.h>
#include <iostream>
#include <algorithm>
#include <iomanip>
#include <math.h>
#pragma GCC optimize (3)//讓我們一起來1*1
using namespace std;
long long int a1[4001],b1[4001],n,m,l,k,d;//a1,b1兩個陣列來儲存橫排與縱排的各個座標上的會進行交頭接耳的人，剩下的儘量按題目的變數命名
long long int a2[4001],b2[4001];//排序要用的陣列
int main()
{
	ios::sync_with_stdio(false);//讓我們一起來省時間*2
	//freopen("seat.in","r",stdin);
	//freopen("seat.out","w",stdout);
	register long long int i,j;//讓我們來一起來省時間*3
	static long long int s;
	cin>>n>>m;
	cin>>k>>l>>d;
	for(i=1,j=1;i<=d;i++)
	{
		int x1,y1,x,y;
		cin>>x>>y>>x1>>y1;
		if(x==x1)//辨別是縱向還是橫向，若橫向相同則分離線為縱向 
		{
			if(y<y1)//這是這兩排的價值
			{
				a1[y]++;
			}
			else//這就相當取min了
			{
				a1[y1]++;
			}
		}
		else if(y==y1)//同理 
		{
			if(x<x1)
			{
				b1[x]++;
			}
			else
			{
				b1[x1]++;
			}
		}
	}
	int x(0),maxn(0);
	for(i=1;i<=k;i++)//將人數最多的K個找出來
	{
		maxn=0;//為了求出每次的最大值，需要每次掃一遍
		x=0;
		for(j=1;j<=m;j++)
		{
			if(b1[j]>maxn)
			{
				maxn=b1[j];
				x=j;
			}
		}
		a2[i]=x;
		b1[x]=0;//要清理，否則接下來都是一個答案 
	}
	for(i=1;i<=l;i++)//將人數最多L個找出來
	{
		maxn=0;
		x=0;
		for(j=1;j<=n;j++)
		{
			if(a1[j]>maxn)
			{
				maxn=a1[j];
				x=j;
			}
		}
		b2[i]=x;
		a1[x]=0;
	}
	sort(a2+1,a2+k+1);//這裡是貪心，找到可以隔開人數最多的路，那麼說話的人就少了 
	sort(b2+1,b2+l+1);
	for(i=1;i<=k;i++)//輸出行最優解
	{
		cout<<a2[i]<<' ';
	}
	cout<<endl;
	for(i=1;i<=l;i++)//輸出列最優解
	{
		cout<<b2[i]<<' ';
	}
	cout<<endl;
	//fclose(stdin);
	//fclose(stdout);
	return 0;
}