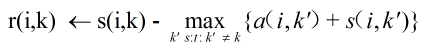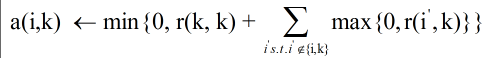演算法概述

原文：
[Frey B J, Dueck D. Clustering by passing messages between data points[J]. science, 2007, 315(5814): 972-976.](Frey B J, Dueck D. Clustering by passing messages between data points[J]. science, 2007, 315(5814)
AP聚類一般翻譯為近鄰傳播聚類，07年被提出，其優點有：
1. 不需要制定最終聚類族的個數
2. 已有的資料點作為最終的聚類中心，而不是新生成一個族中心。
3. 模型對資料的初始值不敏感。
4. 對初始相似度矩陣資料的對稱性沒有要求。
5. 相比與k-centers聚類方法，其結果的平方差誤差較小。

基本概念：
* Exemplar範例：即聚類族中心點；
* s(i,j)：資料點i與資料點j的相似度值，一般使用歐氏距離的的負值表示，即s(i,j)值越大表示點i與j的距離越近，AP演算法中理解為資料點j作為資料點i的聚類中心的能力；
* 相似度矩陣：作為演算法的初始化矩陣，n個點就有由n乘n個相似度值組成的矩陣；
* Preference參考度或稱為偏好引數：是相似度矩陣中橫軸縱軸索引相同的點，如s(i,i)，若按歐氏距離計算其值應為0，但在AP聚類中其表示資料點i作為聚類中心的程度，因此不能為0。迭代開始前假設所有點成為聚類中心的能力相同，因此參考度一般設為相似度矩陣中所有值得最小值或者中位數，但是參考度越大則說明個數據點成為聚類中心的能力越強，則最終聚類中心的個數則越多；
* Responsibility，r(i,k)：吸引度資訊，表示資料點k適合作為資料點i的聚類中心的程度；公式如下：

其中a(i,k’)表示除k外其他點對i點的歸屬度值，初始為0；s(i,k’)表示除k外其他點對i的吸引度，即i外其他點都在爭奪i點的 所有權；r(i,k)表示資料點k成為資料點i的聚類中心的累積證明，r(i,k)值大於0，則表示資料點k成為聚類中心的能力強。說明：此時只考慮哪個點k成為點i的聚類中心的可能性最大，但是沒考慮這個吸引度最大的k是否也經常成為其他點的聚類中心（即歸屬度），若點k只是點i的聚類中心，不是其他任何點的聚類中心，則會造成最終聚類中心個數大於實際的中心個數。
* Availability，a(i,k)：歸屬度資訊，表示資料點i選擇資料點k作為其聚類中心的合適程度，公式如下：

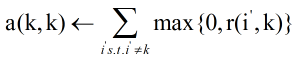
其中r(i’,k)表示點k作為除i外其他點的聚類中心的相似度值，取所有大於等於0的吸引度值，加上k作為聚類中心的可能程。即點k在這些吸引度值大於0的資料點的支援下，資料點i選擇k作為其聚類中心的累積證明。
* Damping factor阻尼係數：為防止資料震盪，引入地衰減係數，每個資訊值等於前一次迭代更新的資訊值的λ倍加上此輪更新值得1-λ倍，其中λ在0-1之間，預設為0.5。

演算法流程：
1. 更新相似度矩陣中每個點的吸引度資訊，計算歸屬度資訊；
2. 更新歸屬度資訊，計算吸引度資訊；
3. 對樣本點的吸引度資訊和歸屬度資訊求和，檢測其選擇聚類中心的決策；若經過若干次迭代之後其聚類中心不變、或者迭代次數超過既定的次數、又或者一個子區域內的關於樣本點的決策經過數次迭代後保持不變，則演算法結束。

關於其演算法流程，知乎上kael 使用者將AP聚類過程比喻為選舉過程：
* 所有人都參加選舉（大家都是選民也都是參選人），要選出幾個作為代表
* s(i,k)就相當於i對選k這個人的一個固有的偏好程度
* r(i,k)表示用s(i,k)減去最強競爭者的評分，可以理解為k在對i這個選民的競爭中的優勢程度
* r(i,k)的更新過程對應選民i對各個參選人的挑選（越出眾越有吸引力）
* a(i,k)：從公式裡可以看到，所有r(i’,k)>0的值都對a有正的加成。對應到我們這個比喻中，就相當於選民i通過網上關於k的民意調檢視到：有很多人（即i’們）都覺得k不錯（r(i’,k)>0），那麼選民i也就會相應地覺得k不錯，是個可以相信的選擇
* a(i,k)的更新過程對應關於參選人k的民意調查對於選民i的影響（已經有了很多跟隨者的人更有吸引力）
* 兩者交替的過程也就可以理解為選民在各個參選人之間不斷地比較和不斷地參考各個參選人給出的民意調查。
* r(i,k)的思想反映的是競爭，a(i,k)則是為了讓聚類更成功。
作者：kael
連結：https://www.zhihu.com/question/25384514/answer/47636054

演算法缺點：
1. 雖然AP演算法不用提前設定聚類中心的個數，但是需要事先設定參考度，而參考度的大小與聚類中心的個數正相關；
2. 由於AP演算法每次迭代都需要更新每個資料點的吸引度值和歸屬度值，演算法複雜度較高，在大資料量下執行時間較長。

演算法應用：
工具：
Python語言的機器學習庫scikit-learn；
* win7-64位下安裝scikit-learn：
1. 需要環境
Python (>= 2.6 or >= 3.3),
NumPy (>= 1.6.1),
SciPy (>= 0.9).
可以使用pip安裝NumPy和NumPy，也可以直接安裝Python(x,y) 即滿足scikit-learn的安裝環境；
2. cmd調出命令輸入介面後，輸入pip install -U scikit-learn，即可完成安裝；
3. 除此之外，Python科學計算整合開發環境Anaconda中已經自帶最新版的scikit-learn包。
* 示例：

from sklearn.cluster import AffinityPropagation
from sklearn import metrics
from sklearn.datasets.samples_generator import make_blobs
# 生成測試資料
centers = [[1, 1], [-1, -1], [1, -1]]
# 生成實際中心為centers的測試樣本300個，X是包含300個(x,y)點的二維陣列，labels_true為其對應的真是類別標籤
X, labels_true = make_blobs(n_samples=300, centers=centers, cluster_std=0.5,
                            random_state=0)    

# 計算AP
ap = AffinityPropagation(preference=-50).fit(X)
cluster_centers_indices = ap.cluster_centers_indices_    # 預測出的中心點的索引，如[123,23,34]
labels = ap.labels_    # 預測出的每個資料的類別標籤,labels是一個NumPy陣列

n_clusters_ = len(cluster_centers_indices)    # 預測聚類中心的個數

print('預測的聚類中心個數：%d' % n_clusters_)
print('同質性：%0.3f' % metrics.homogeneity_score(labels_true, labels))
print('完整性：%0.3f' % metrics.completeness_score(labels_true, labels))
print('V-值： % 0.3f' % metrics.v_measure_score(labels_true, labels))
print('調整後的蘭德指數：%0.3f' % metrics.adjusted_rand_score(labels_true, labels))
print('調整後的互資訊： %0.3f' % metrics.adjusted_mutual_info_score(labels_true, labels))
print('輪廓係數：%0.3f' % metrics.silhouette_score(X, labels, metric='sqeuclidean'))

# 繪製圖表展示
import matplotlib.pyplot as plt
from itertools import cycle

plt.close('all')    # 關閉所有的圖形
plt.figure(1)    # 產生一個新的圖形
plt.clf()    # 清空當前的圖形

colors = cycle('bgrcmykbgrcmykbgrcmykbgrcmyk')
# 迴圈為每個類標記不同的顏色
for k, col in zip(range(n_clusters_), colors):
    # labels == k 使用k與labels陣列中的每個值進行比較
    # 如labels = [1,0],k=0,則‘labels==k’的結果為[False, True]
    class_members = labels == k
    cluster_center = X[cluster_centers_indices[k]]    # 聚類中心的座標
    plt.plot(X[class_members, 0], X[class_members, 1], col + '.')
    plt.plot(cluster_center[0], cluster_center[1], markerfacecolor=col,
             markeredgecolor='k', markersize=14)
    for x in X[class_members]:
        plt.plot([cluster_center[0], x[0]], [cluster_center[1], x[1]], col)

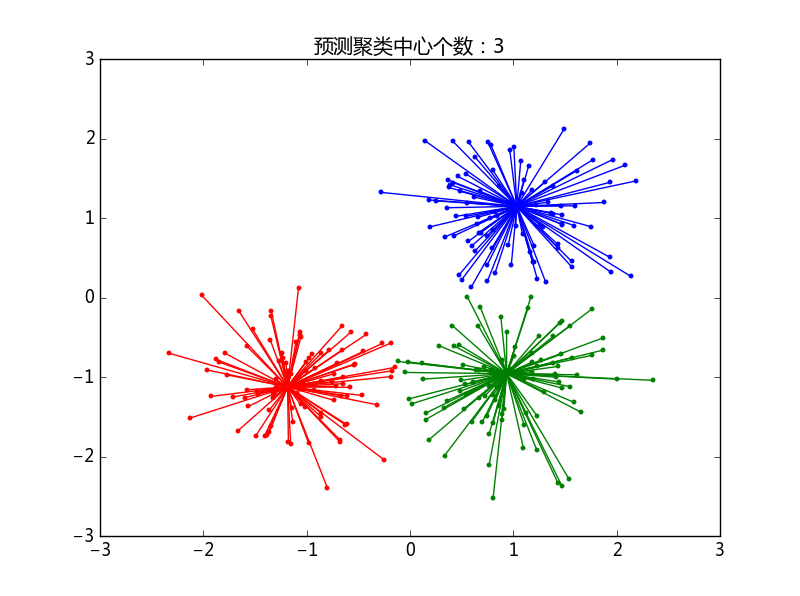
plt.title('預測聚類中心個數：%d' % n_clusters_)
plt.show()```

測試結果：  

預測的聚類中心個數：3
同質性：0.872
完整性：0.872
V-值： 0.872
調整後的蘭德指數：0.912
調整後的互資訊： 0.871
輪廓係數：0.753
“`