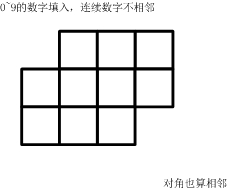
如圖，如下的10個格子，填入0~9的數字。要求：連續的兩個數字不能相鄰。
（左右、上下、對角都算相鄰）一共有多少種可能的填數方案？
請填寫表示方案數目的整數。

看到這題第一個想到的方法就是回溯，就很像八皇后，能填進去就填，填不進去就看下一個位置（我做的是0---9不重複使用）

我感覺這題麻煩就在判斷上

1.首先要判斷一個點的8個方向相減的絕對值是否為1，為1不能填入，不為1判斷是否使用過這個數，沒使用填入 進行下一個位置

2.如果填入的位置到達最後一列應該換行看下一行的第一個位置進行判斷

3.填到最後每一個情況總sum++就行了

上程式碼

#include<iostream>
using namespace std;
int a[3][4];
int num = 0;
int v[10] = {0};
int pd(int k, int i, int j){//這個就是判斷啦。。寫的有點繁瑣
	if (i-1>=0 && (a[i - 1][j] == k - 1 || a[i - 1][j] == k + 1) )
		return 0;
	if (j-1>=0 && (a[i][j - 1] == k + 1 || a[i][j - 1] == k - 1) )
		return 0;
	if (i-1>=0 && j-1>=0 && (a[i - 1][j - 1] == k + 1 || a[i - 1][j - 1] == k - 1))
		return 0;
	if (i-1>=0 && j+1<4 && (a[i - 1][j + 1] == k + 1 || a[i - 1][j + 1] == k - 1))
		return 0;
	if (j + 1 < 4 && (a[i][j + 1] == k + 1 || a[i][j + 1] == k - 1))
		return 0;
	if (i + 1 < 3 && (a[i + 1][j] == k + 1 || a[i + 1][j] == k - 1))
		return 0;
	if (i + 1 < 3 && j - 1 >= 0 && (a[i + 1][j - 1] == k + 1 || a[i + 1][j - 1] == k - 1))
		return 0;
	if (i + 1 < 3 && j + 1 < 4 && (a[i + 1][j + 1] == k + 1 || a[i + 1][j + 1] == k - 1))
		return 0;
	return 1;
}
void f(int i, int j){
	if (i == 2&&j==3){//已經填入到最後一個說明這種情況滿足，num++
		num++;
		return;
	}
		for (int k = 0; k <= 9; k++){
			if (pd(k, i, j)&&v[k]==0) {//判斷8個方向是否能填入，並且是否用過
				v[k] = 1;
				a[i][j] = k;
				if (j == 3)//到達最後一列記得換行
					f(i + 1, 0);
				else
					f(i, j + 1);
				a[i][j] = -9;
				v[k] = 0;
			}
		}
}
int main(){
	for (int i = 0; i < 3; i++)//這裡我將所有數賦值-9，因為第一個和最後一個不需要賦值，避免干擾
		for (int j = 0; j < 4; j++)
			a[i][j] = -9;
	f(0, 1);
	printf("%d", num);
	return 0;
}
 

結果應該是：1580

理解了八皇后這個典型的回溯，這些都不太麻煩了

歡迎大家加入 早起學習群，一起學習一起進步！（群號：642179511）