無監督學習之K-均值演算法分析與MATLAB程式碼實現
前言
K-均值是一種無監督的聚類演算法。首先我們要知道什麼是無監督,無監督就是說在資料集中,資料是沒有標籤的。在有監督的資料集中,資料的形式可能是這樣:
無監督學習一般用來做什麼呢?比如市場分割,也許在你的資料庫中有很多使用者的資料,你希望將使用者分成不同的客戶群,這樣對不同型別的客戶你可以分別提供更合適的服務。再比如圖片壓縮,假如圖片有256種顏色,我們想用16種來表示,那麼我們也可以用聚類的方式來將256種顏色分成16類。
K-均值演算法
而K-均值是一個很普遍的聚類演算法。這個演算法接受一個未標記的資料集,然後將資料集聚類成不同的組。
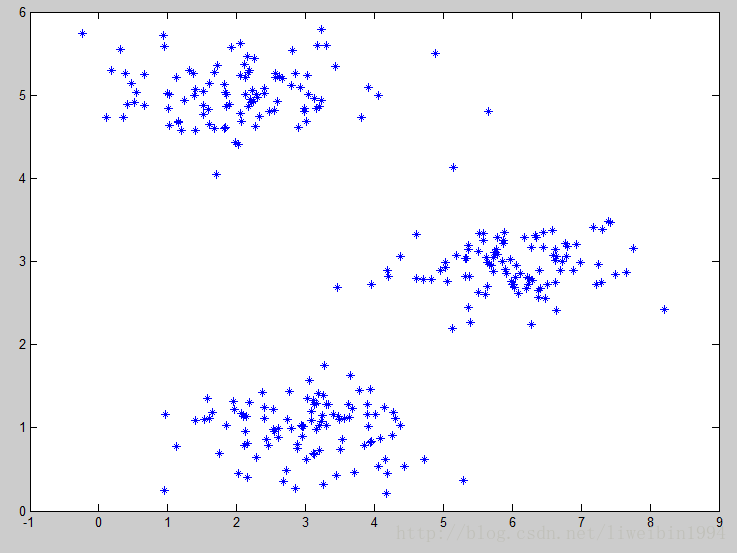
如上圖所示,我們可以很直觀地看出資料集大致可以分成三類,K-均值演算法的思想就是選擇三個隨機的點(當然,分成K類就K個隨機的點),稱為聚類中心(cluster centroids)。
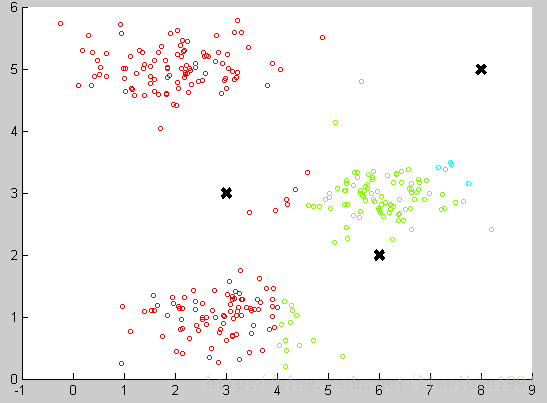
然後對於資料集中的每一個數據,按照距離三個中心點的距離,將其與距離最近的中心點關聯起來,與同一個中心點關聯的所有點聚成一類。如下圖:
圖中三個黑色的點就是三個聚類中心,資料集也根據與聚類中心的遠近分成三組。可以看出,此時的分類還是不好的。那麼我們接下來應該怎麼做才能讓這個分類效果更好呢?
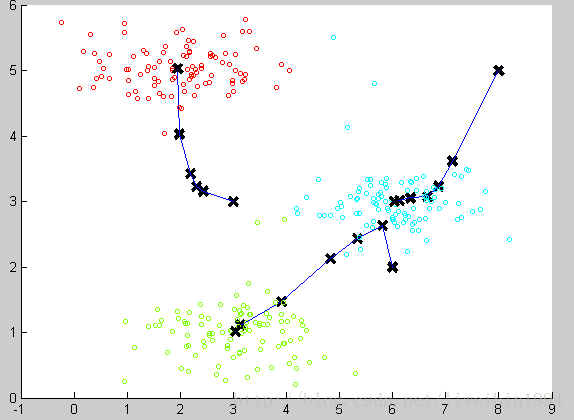
我們可以計算每個組(資料集被分成紅綠藍這三個組)的資料的平均值,將該組所關聯的中心點移動到平均值的位置。
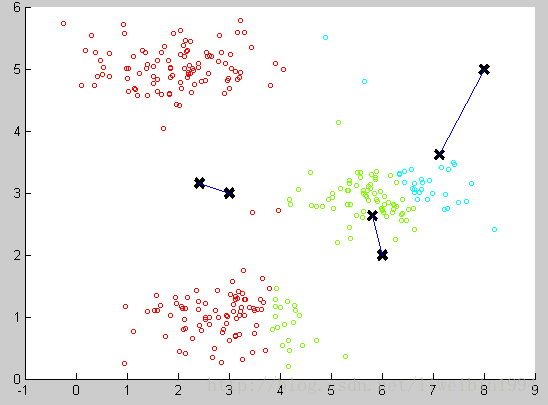
通過計算平均值,將聚類中心移動到平均值所在的位置,然後我們重複這個過程,直到中心點不再變化。最後就可以得到下面的效果:
可以看到聚類的效果還不錯。
演算法步驟與虛擬碼
根據上面的分析,演算法的步驟可以歸結為:
第一步,隨機選擇三個點,假設為A,B,C;
第二步:計算資料集中的每個資料
第三步,計算三組類別的資料的均值,分別作為A,B,C的新位置。
第四步,重複第二步和第三步直到迭代結束或者A,B,C的位置不再移動。
K-均值的虛擬碼如下:
用
Repeat{
for i=1 to m
for k = 1 to K
}
優化目標(代價函式)
K-均值最小化問題,是要最小化所有的資料點與其關聯的聚類中心之間的距離之和。因此,K-均值的代價函式:
其中,
上面的虛擬碼中,第一個for迴圈就是用於減少
第二個迴圈則是用於減小
初始化問題
在上面的步驟分析中,執行K-均值演算法之前,我們首先要隨機初始化所有的聚類中心。如何初始化比較好呢?
- 首先,應該選擇K < m,也就是聚類中心的個數要小於所有訓練集例項的數量。
- 隨機選擇K個訓練樣本,然後令K個聚類中心分別與這K個訓練樣本相等。
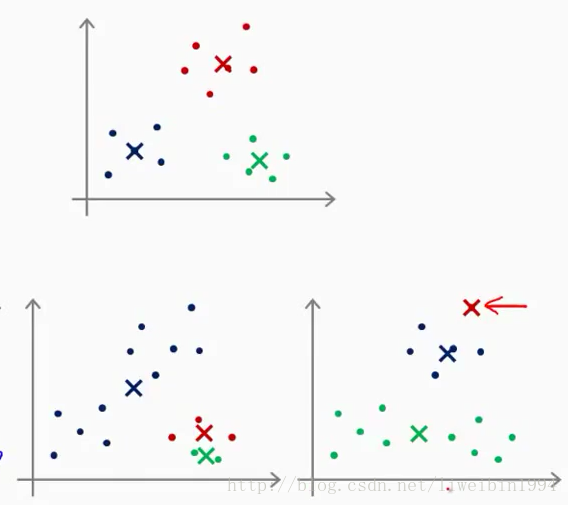
上面一開始說隨機取K個點這種做法其實不推薦。K-均值的一個問題就在於,它有可能會停留在一個區域性最小值處,而這取決於初始化的情況。
圖中上面一個座標系是分類正常,下面兩個都是分類不好的情況。為了解決這個問題,我們通常需要多次執行K-均值演算法,每一次都重新進行隨機初始化,最後再比較多次執行K-均值的結果,選擇代價函式最小的結果。這種方法在K較小的時候(2~10)還是可行的,但是如果K較大,這麼做也可能不會有明顯的效果。
K的選擇
其實沒有所謂的最好的選擇聚類數K的方法,通常是根據不同的問題,人工進行選擇的。選擇的時候思考我們運用K-均值演算法聚類的動機是什麼,然後選擇能最好服務於該目的的聚類數。
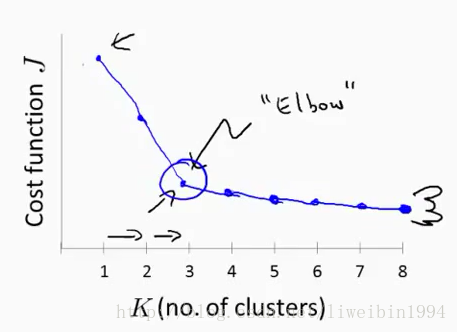
肘部法則
一般來說,人們可能會用肘部法則來選擇K。這個法則的做法就是改變K值,然後每次改變之後我們執行一下演算法,得到代價函式J的值,然後畫影象:
橫座標是K的數量,縱座標是代價J。經過上面的做法我們可能會得到圖中所示的曲線。這條曲線像人的肘部,所以叫肘部法則。在這種模式下(曲線下),隨著K的增加,代價函式的值會迅速減小,然後趨於平緩。所以我們一般就會選擇拐點對應的K值來作為聚類數。