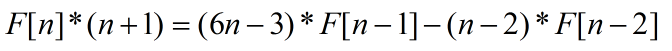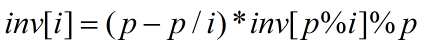超級卡特蘭數(bzoj 4706: B君的多邊形)
阿新 • • 發佈:2019-02-11
Submit: 159 Solved: 92
[Submit][Status][Discuss]
Description
有一個正n多邊形,我們要連線一些對角線,把這個多邊形分成若干個區域。要求連線的對角線不能相交,每個點可以連出也可以不連出對角線。(即最終不要求所有區域均為三角形)問總方案數mod (10^9+7)的結果。Input
一行一個整數n,n≤10^6Output
一行一個整數表示答案。Sample Input
5Sample Output
11超級卡特蘭數(又稱大施羅德數):
公式:
前幾項: 1, 1, 3, 11, 45, 197, 903, 4279, 20793, 103049, 518859, 2646723, 13648869, 71039373, 372693519, 1968801519, 10463578353, 55909013009, 300159426963, 1618362158587, 8759309660445, 47574827600981, 259215937709463……
功能:應該和卡特蘭數一樣有很多的應用比如這題,但是很少見到有這個說法,也不清楚其他的例子,比較神祕的序列,就先記下遞推公式和前幾項吧
附:快速求逆元的方法:
令inv[i]表示i對p的逆元(p為奇質數),
#include<stdio.h> #define LL long long #define mod 1000000007 LL inv[1000005] = {1,1}, f[1000005] = {1,1}; int main(void) { int n, i; scanf("%d", &n); for(i=2;i<=n;i++) inv[i] = (mod-mod/i)*inv[mod%i]%mod; for(i=2;i<=n;i++) f[i] = ((6*i-3)*f[i-1]%mod-(i-2)*f[i-2]%mod+mod)%mod*inv[i+1]%mod; printf("%lld\n", f[n-2]); }