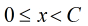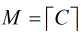現在我來介紹一種演算法叫做Baby Step Giant Step。它是用來解決如下方程最小正整數解的

           其中

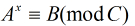
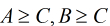
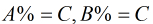
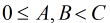
如果，那麼我們可以先取模，即，所以在這裡我們只討論的情況。

普通Baby Step Giant Step的步驟是這樣的：

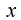
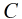
    （1）首先確定的下限是0，上限是，我們令

    （2）把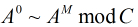的值存到一個Hash表裡面

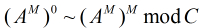
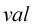
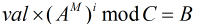
    （3）把的值一一枚舉出來，每列舉一個就在Hash表裡面尋找是否有一個值滿足

        ，如果有則找到答案，否則繼續

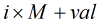
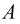
    （4）最終答案就是的值對應的原來的冪

     上面是普通Baby Step Giant Step的步驟，比較簡單，只適用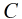

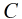
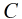
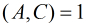
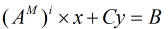
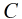
當為合數時，我們就需要把Baby Step Giant Step擴充套件一下。在普通Baby Step Giant Step中，由於是素數，那麼，所以一定有唯一解的。那麼，當為合數時，我們可以這樣處理：

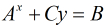
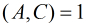
對於方程，我們拿出若干個出來與來消去公共因子，使得為止，那麼此時我們就可以直接通過擴充套件歐幾里得來計算結果了。

#include <iostream>
#include <string.h>
#include <stdio.h>
#include <math.h>

using namespace std;
typedef long long LL;

const int MOD = 99991;
const int N = 100005;

struct Hash
{
    bool f;
    int id;
    int val;
};

Hash hash[N];

void Init()
{
    for(int i=0; i<N; i++)
    {
        hash[i].f = 0;
        hash[i].id = -1;
        hash[i].val = -1;
    }
}

void Insert(int id,LL val)
{
    LL t = val % MOD;
    while(hash[t].f && hash[t].val != val)
    {
        t++;
        t %= MOD;
    }
    if(!hash[t].f)
    {
        hash[t].f = 1;
        hash[t].id = id;
        hash[t].val = val;
    }
}

int Find(LL val)
{
    LL t = val % MOD;
    while(hash[t].f && hash[t].val != val)
    {
        t++;
        t %= MOD;
    }
    if(!hash[t].f) return -1;
    return hash[t].id;
}

LL gcd(LL a,LL b)
{
    return b ? gcd(b,a%b):a;
}

void extend_Euclid(LL a,LL b,LL &x,LL &y)
{
    if(b == 0)
    {
        x = 1;
        y = 0;
        return;
    }
    extend_Euclid(b,a%b,x,y);
    LL tmp = x;
    x = y;
    y = tmp - (a / b) * y;
}

LL Baby_Step(LL A,LL B,LL C)
{
    LL ret = 1;
    for(int i=0; i<=50; i++)
    {
        if(ret == B) return i;
        ret = ret * A % C;
    }
    LL ans = 1;
    LL tmp,cnt = 0;
    while((tmp = gcd(A,C)) != 1)
    {
        if(B % tmp) return -1;
        B /= tmp;
        C /= tmp;
        ans = ans * (A / tmp) % C;
        cnt++;
    }
    LL M = ceil(sqrt(1.0*C));
    LL t = 1;
    for(int i=0; i<M; i++)
    {
        Insert(i,t);
        t = t * A % C;
    }
    for(int i=0; i<M; i++)
    {
        LL x,y;
        extend_Euclid(ans,C,x,y);
        LL val = x * B % C;
        val = (val % C + C) % C;
        LL j = Find(val);
        if(j != -1) return i * M + j + cnt;
        ans = ans * t % C;
    }
    return -1;
}

int main()
{
    LL A,B,C;
    while(cin>>A>>C>>B)
    {
        Init();
        if(A + B + C == 0) break;
        A %= C; B %= C;
        LL ans = Baby_Step(A,B,C);
        if(ans == -1)
        {
            puts("No Solution");
            continue;
        }
        cout<<ans<<endl;
    }
    return 0;
}