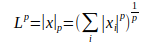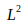範數(norm)
範數,在機器學習中通常用於衡量一個向量的大小,形式上,
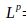
其中 p>=1
從巨集觀上來講,範數是將向量對映到非負值的函式,從直觀上來說,範數是向量x到原點的距離。
但是範數並不侷限於上述的公式,對任意的函式只要滿足以下的性質,則可以稱該函式是範數:
1)對於 f(x) = 0,則一定有x = 0
2) f(x + y) <= f(x) + f(y)
3)對任意的標量a,一定有 f(ax) = |a| f(x)
注意:以上性質中,x與y都是向量。
當p = 2時,
常用的範數形式,除了上述的歐幾里得範數,還有用於統計向量中非零元素個數的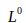
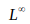
有時候,我們也需要表示矩陣的大小,在深度學習中,我們通常用Frobenius範數來衡量一個矩陣的大小,計算公式如下:
相關推薦
向量範數與矩陣範數norm 向量範數與矩陣範數
轉 向量範數與矩陣範數 2016年07月18日 20:35:26 bitcarmanlee 閱讀數:42662 &l
範數(norm)
範數,在機器學習中通常用於衡量一個向量的大小,形式上, 範數的定義如下: 其中 p>=1 從巨集觀上來講,範數是將向量對映到非負值的函式,從直觀上來說,範數是向量x到原點的距離。 但是範數並不侷限於上述的公式,對任意
numpy.linalg.norm(求範數)
inf none 線性 ron image .com 多個 port print 1、linalg=linear(線性)+algebra(代數),norm則表示範數。 2、函數參數 x_norm=np.linalg.norm(x, ord=None, axis=None,
Frobenius norm(Frobenius 範數)
http span orm inf 分享圖片 9.png com clas class Frobenius 範數,簡稱F-範數,是一種矩陣範數,記為||·||F。 矩陣A的Frobenius範數定義為矩陣A各項元素的絕對值平方的總和,即 可用於
【 MATLAB 】norm ( Vector and matrix norms )(向量範數以及矩陣範數)
norm Vector and matrix norms Syntax n = norm(v) n = norm(v,p) n = norm(X) n = norm(X,p) n = norm(X,'fro') Description n = norm
matlab norm向量和矩陣的範數
一、向量的範數 首先定義一個向量為:a=[-5,6,8, -10] 1.1 向量的1範數 向量的1範數即:向量的各個元素的絕對值之和,上述向量a的1範數結果就是:29,MATLAB程式碼實現為:norm(a,1); 1.2
深度學習基礎--正則化與norm--L1範數與L2範數的聯絡
L1範數與L2範數的聯絡 假設需要求解的目標函式為:E(x) = f(x) + r(x) 其中f(x)為損失函式,用來評價模型訓練損失,必須是任意的可微凸函式,r(x)為規範化約束因子,用來對模型進行限制。 根據模型引數的概率分佈不同,r(x)一般有: 1)L1正規化
python數值計算庫Numpy學習之—np.linalg.norm(求範數)
Numpy在python中是非常著名的一個數值計算型別的庫,線上性代數裡面的矩陣求和、求逆、求距離、求範數等等,都有很友好的支援,今天正好再一次用到了它的範數求解操作,就專門找一點時間總結了一下,備忘,下面是具體的實現,引數解釋以及程式碼註釋都已經比較詳細了就不多再解釋了
steepest descent for Euclidean norm 最速下降法中二次範數的下降方向
在無約束優化中,設f(x)f(x)f(x)是凸函式。可以通過∂f(x)=0\partial f(x)=0∂f(x)=0求解,如果不能直接得到解析解,可以通過構造一個序列,x0,x1,...,xkx_0,x_1,...,x_kx0,x1,...,xk,使得f
向量與矩陣的範數及其在matlab中的用法(norm)
一、常數向量範數 L0範數 ∥x∥0=def‖x‖0=def向量中非零元素的個數 其在matlab中的用法: sum( x(:) ~= 0 ) L1範數 ∥x∥1=def∑i=1m|xi|=|x1|+⋯+|xm|‖x‖1=def∑i=1m|xi|=|x1|
Huber Norm:Huber 範數
最近在看論文的時候遇到了一個術語:Huber 範數,百度之,卻沒有搜到相關的資料。經過探究,實質上,在機器學習領域,Huber 範數一般指的是Huber Loss(Huber 損失),是一種與L2範數類似的,衡量誤差的方法。 Huberα(x)={x22α
矩陣範數(martix norm) --維基百科
矩陣範數(martix norm)是數學上向量範數對矩陣的一個自然推廣。 [編輯]矩陣範數的特性 以下K代表實數或複數域。現在考慮空間,亦即所有m行與n列的矩陣。 上的矩陣範數滿足向量範數的所有特性,即若是矩陣A的範數,那麼: ,且等號成立當且僅當A= 0。,對
範數(norm)
不說那麼多理論了,弄蒙咋整,直接說常見範數及其用途。 一、向量範數 1.1、 0-範數 嚴格說不屬於範數,向量中非零元素的個數。 1.2、 1-範數 即向量元素絕對值之和,matlab呼叫函式norm(x, 1) 。 1.3、 2-範數 Euclid範數(歐幾里得範數,
opencv裡的norm範數和影象裡的深度和通道數的理解和意義和相機標定後對內外引數的質量評估
CV_8UC1 是指一個8位無符號整型單通道矩陣, CV_32FC2是指一個32位浮點型雙通道矩陣 CV_8UC1 CV_8SC1 CV_16U C1 CV_16SC1 CV_8UC2 CV_
什麽是矩陣的範數【轉載】
log 一次函數 絕對值 半徑 領域 理解 思維 tro 函數 在介紹主題之前,先來談一個非常重要的數學思維方法:幾何方法。在大學之前,我們學習過一次函數、二次函數、三角函數、指數函數、對數函數等,方程則是求函數的零點;到了大學,我們學微積分、復變函數、實變函數、泛函等。我
機器學習中的範數規則化之(一)L0、L1與L2範數
[0 證明 基本上 復雜度 所有 img 方法 風險 機器學習 機器學習中的範數規則化之(一)L0、L1與L2範數 [email protected]/* */ http://blog.csdn.net/zouxy09 轉自:http://blog.csdn.n
『教程』L0、L1與L2範數_簡化理解
線性 實驗 tab 下一個 約束 特征 方式 等於 b2c 『教程』L0、L1與L2範數 一、L0範數、L1範數、參數稀疏 L0範數是指向量中非0的元素的個數。如果我們用L0範數來規則化一個參數矩陣W的話,就是希望W的大部分元素都是0,換句話說,讓參數W
向量範數和矩陣範數
-m des ash comm pat 矩陣 status edi src 原文:https://www.zhihu.com/question/20473040以下分別列舉常用的向量範數和矩陣範數的定義。 向量範數 1-範數: ,即向
矩陣範數
以及 span lambda mit 一點 rep logs body 估計 將學習到什麽 矩陣範數相關. ? 基礎 ? 函數 \(\lVert \cdot \rVert\):\(M_n \rightarrow \mathbb{R}\) 稱為一個矩陣範數,如果對所有 \(
【轉】範數規則化L0、L1與L2範數
spa http span get font lan pan href -s http://blog.csdn.net/zouxy09/article/details/24971995【轉】範數規則化L0、L1與L2範數