比來看了些主成分解析，混跡Matlab論壇，翻了n多帖子，對princomp函式有了些懂得。

在此只講一些小我懂得，並沒有效術語，只求通俗。

供獻率：每一維資料對於區分全部資料的供獻，供獻率最大的顯然是主成分，第二大的是次主成分......

[coef，score，latent，t2] = princomp（x）;（小我概念）：

x：為要輸入的n維原始資料。帶入這個matlab自帶函式，將會生成新的n維加工後的資料（即score）。此資料與之前的n維原始資料一一對應。

score：生成的n維加工後的資料存在score裡。它是對原始資料進行的解析，進而在新的座標系下獲得的資料。他將這n維資料按供獻率由大到小分列。（即在改變座標系的景象下，又對n維資料排序）

latent：是一維列向量，每一個數據是對應score裡響應維的供獻率，因為數佔領n維所以列向量有n個數據。由大到小分列（因為score也是按供獻率由大到小分列）。

coef：是係數矩陣。經由過程cofe可以知道x是如何轉換成score的。

則模型為從原始資料出發：score= bsxfun（＠minus，x，mean（x，1））*coef;（感化：可以把測試資料經由過程此辦法改變為新的座標系）

逆變換：x= bsxfun（＠plus，score*inv（coef），mean（x，1））



例子：

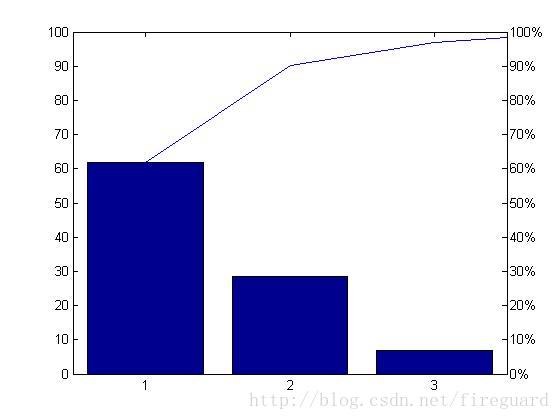
％％％清屏
clear
％％％初始化資料
a=[-14.8271317103068
 
，-3.00108550936016，1.52090778549498，3.95534842970601;-16.2288612441648，-2.80187433749996，-0.410815700402130，1.47546694457079;-15.1242838039605，-2.59871263957451，-0.359965674446737，1.34583763509479;-15.7031424565913，-2.53005662064257，0.255003254103276，-0.179334985754377;-17.7892158910100，-3.32842422986555，0.255791146332054，1.65118282449042
 
;-17.8126324036279，-4.09719527953407，-0.879821957489877，-0.196675865428539;-14.9958877514765，-3.90753364293621，-0.418298866141441，-0.278063876667954;-15.5246706309866，-2.08905845264568，-1.16425848541704，-1.16976057326753;];
x=a;
％％％呼叫princomp函式
[coef，score，latent，t2] = princomp（x）;
score
％測試score是否和score_test一樣
score_test=bsxfun（＠minus，x，mean（x，1））*coef;
score_test

latent=100*latent/sum（latent）％將latent總和同一為100，便於調查供獻率
pareto（latent）;％呼叫matla畫圖

上圖是經由過程自帶函式繪製，當供獻率累加至95％，今後的維數會不在顯示，最多隻顯示10維。

下面用本身編寫的默示：

之前的錯誤熟悉：

1.認為主成分解析中latent顯示的供獻值是原始資料的，其實是加工後的資料的。申明:對原始資料既然選擇PCA辦法，那麼策畫機認為原始資料每維之間可能存在接洽關係，你想去掉接洽關係、降落維數。所以採取這種辦法的。所以策畫機並不關懷原始資料的供獻值，因為你不會去用了，用的是加工後的資料（這也是為什麼當把輸入資料每一維的次序改變後，score、latent不受影響的原因）。

2.認為PCA解析後主動降維，不合錯誤。PCA後會有供獻值，是輸入者按照本身想要的供獻值進行維數的改變，進而生成資料。（一般大師會取供獻值在85％以上，請求高一點95％）。

3.PCA解析，只按照輸入資料的特點進行主成分解析，與輸出有幾許型別，每個資料對應哪個型別無關。若是樣本已經分好型別，那PCA後勢必對成果的正確性有必然影響，我認為對於此類資料的PCA，就是在降維與正確性間找一個均衡點的題目，讓資料即不會維數多而使運算錯雜，又有較高的辨別率。