已知一個成本矩陣cost[][]，位置(m, n)的權重是cost[][]，寫一個函式，這個函式返回從(0, 0)到(m, n)的最小帶權路徑。矩陣的每個格子表示的是通過這個格子的代價。到達(m, n)的路徑總代價是這條路上所有代價和（包括出發點和終點）。你只可以從當前的格子向下，向右，或者對角線移動到下面的格子。例如給定(i, j)，只可以移動到cells (i+1, j)，(i, j+1) 和(i+1, j+1)。你可以假設所有的成本都是正整數。

例如，在下面的圖中，到(2, 2)的最小帶權路徑是啥？

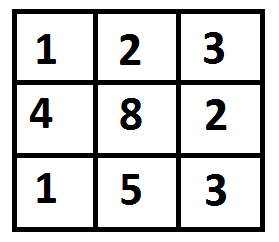
最小帶權路徑在下面的圖中已經標記出來了，路徑是(0, 0) –> (0, 1) –> (1, 2) –> (2, 2)。路徑的成本是8 (1 + 2 + 2 + 3)。

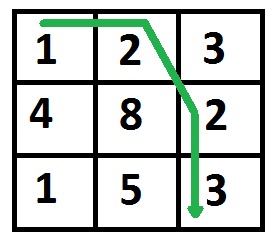
1）最優的子結構
到達 (m, n) 的路徑必須通過下面三個格子中的一個：(m-1, n-1)或者(m-1, n)或者(m, n-1)。所以到達(m, n)的最小成本快一些寫成“到達三個格子的最小值加上cost[m][n]”。

minCost(m, n) = min (minCost(m-1, n-1), minCost(m-1, n), minCost(m, n-1)) + cost[m][n]

2）重複的子問題
下面是MCP（Minimum Cost Path）問題的一個比較簡單的遞迴實現了。這個實現就是根據上面的遞迴結構來寫的。

/* A Naive recursive implementation of MCP(Minimum Cost Path) problem */
 

#include<stdio.h>
#include<limits.h>
#define R 3
#define C 3

int min(int x, int y, int z);

/* Returns cost of minimum cost path from (0,0) to (m, n) in mat[R][C]*/
int minCost(int cost[R][C], int m, int n)
{
   if (n < 0 || m < 0)
      return INT_MAX;
   else if (m == 0 && n == 0
 
)
      return cost[m][n];
   else
      return cost[m][n] + min( minCost(cost, m-1, n-1),
                               minCost(cost, m-1, n), 
                               minCost(cost, m, n-1) );
}

/* A utility function that returns minimum of 3 integers */
int min(int x, int y, int z)
{
   if (x < y)
      return (x < z)? x : z;
   else
      return (y < z)? y : z;
}

/* Driver program to test above functions */
int main()
{
   int cost[R][C] = { {1, 2, 3},
                      {4, 8, 2},
                      {1, 5, 3} };
   printf(" %d ", minCost(cost, 2, 2));
   return 0;
}

應該注意的是，上面的方法重複計算了一些子問題，看下面這個遞迴樹，有許多節點出現了多次，這個遞迴的時間複雜度是指數級的，執行起來超慢。

mC refers to minCost()
                                    mC(2, 2)
                          /            |           \
                         /             |            \             
                 mC(1, 1)           mC(1, 2)             mC(2, 1)
              /     |     \       /     |     \           /     |     \ 
             /      |      \     /      |      \         /      |       \
       mC(0,0) mC(0,1) mC(1,0) mC(0,1) mC(0,2) mC(1,1) mC(1,0) mC(1,1) mC(2,0) 

所以MCP問題有動態規劃的兩個屬性（重複子問題與最優子結構），就像其他典型的DP問題一樣，可以通過自底向上地構建一個臨時陣列tc[][]來避免重複計算相同的子問題。

/* Dynamic Programming implementation of MCP problem */
#include<stdio.h>
#include<limits.h>
#define R 3
#define C 3

int min(int x, int y, int z);

int minCost(int cost[R][C], int m, int n)
{
     int i, j;

     // Instead of following line, we can use int tc[m+1][n+1] or 
     // dynamically allocate memoery to save space. The following line is
     // used to keep te program simple and make it working on all compilers.
     int tc[R][C];  

     tc[0][0] = cost[0][0];

     /* Initialize first column of total cost(tc) array */
     for (i = 1; i <= m; i++)
        tc[i][0] = tc[i-1][0] + cost[i][0];

     /* Initialize first row of tc array */
     for (j = 1; j <= n; j++)
        tc[0][j] = tc[0][j-1] + cost[0][j];

     /* Construct rest of the tc array */
     for (i = 1; i <= m; i++)
        for (j = 1; j <= n; j++)
            tc[i][j] = min(tc[i-1][j-1], tc[i-1][j], tc[i][j-1]) + cost[i][j];

     return tc[m][n];
}

/* A utility function that returns minimum of 3 integers */
int min(int x, int y, int z)
{
   if (x < y)
      return (x < z)? x : z;
   else
      return (y < z)? y : z;
}

/* Driver program to test above functions */
int main()
{
   int cost[R][C] = { {1, 2, 3},
                      {4, 8, 2},
                      {1, 5, 3} };
   printf(" %d ", minCost(cost, 2, 2));
   return 0;
}

輸出：

8

這個實現的時間複雜度是 O(mn)，這比前面那個簡單的遞迴實現好多了。