Supervised Hashing with Kernels
1. KSH Formulation
Data Samples:
Hashing Function: ,
is the kernel function;
is the weight
for the sample
(similar to SVM,
is the support vector and
is
the coressponding weight);
is the threshold and usualy be median to make
,
usualy use the mean to replace median and
.
Thus, ,
In vector format:
Since completely determines a hash function
, we seek to learn
by leveraging supervised information so that the resulted hash function is discriminative.
Define label matrix:
The purpose of supervised hashing is to make a pair with will have the minimal Hamming distance 0, while a pair with
will take on the maximal Hamming distance.But the hamming distance is nonconvex, directly optimizing is nontrivial. Meanwhile, code inner products are easier to manipulate
and optimize, and the r
,
is the hashing bits.
Thus , and
, let
to
fit
.
Based on the above description, the objective function can be given in least-squares style:
where, denotes the hamming code matrix, and
, and
represents
frobenius norm:
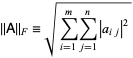
And,
,
Thus the objective function can be rewrited as:
2. Greedy Optimization
The above objective function inspires a greedy idea for solving's sequentially: at a time, it only involves solving one vector
provided
with the previously solved vectors
, ......,
.
Define residue matrix:
Thus, objective function can be rewrited as:
The equivalent optimization problem:
2.1Spectral Relaxation(remove sign() directly)
Based on the above, the objective function is as folows, it is a generalized eigenvalue problem.
is the eigenvector of
, thus
Based on which, will be the eigenvector of
,
and the maximize value will be the largest eigenvalue.
But it might deviate far away from the optimal solution under larger (e.g., ≥ 5,000) due to the amplified relaxation error. It is therefore usedas
the initialization to a more principled optimization scheme as folows.
2.2 Sigmoid Smoothing(replace sign() with sigmoid fun)
Define sigmoid function:
The objective function is:
Use gradient descent to solve the above optimization problem:
3. The pseudo-code of the alogrithm
4. libLBFGS optimization libaray
The library is C implementation of Limited-memory Broyden-Fletcher-Goldfarb-Shanno (L-BFGS) method, use which to solve the above optimization problem.
5. Reference

