MIT演算法導論-第二講-漸進符號,遞迴及解法
阿新 • • 發佈:2019-02-14
1.漸進符號
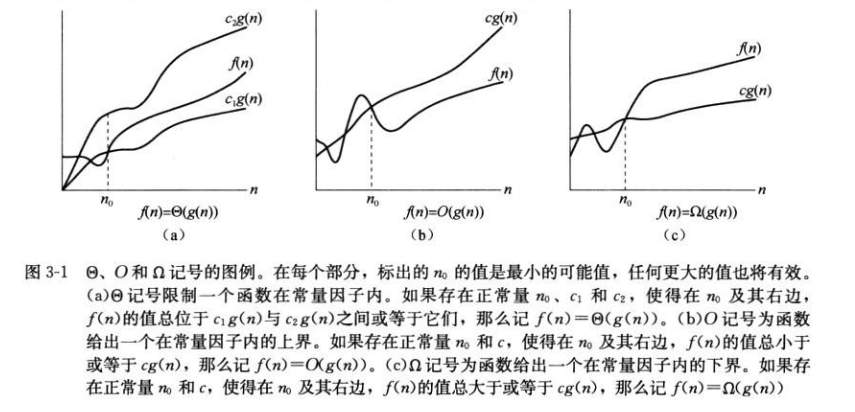
- Θ符號,f(n) = Θ(g(n)),表示f(n)的複雜度既大於等於*g(n)的複雜度,又小於等於g(n)的複雜度,即於g(n)的複雜度相當*。
- O符號,f(n) = O(g(n)),表示f(n)的複雜度最多與g(n)一個數量級,即小於等於。
Ω符號,f(n) = Ω(g(n)),f(n)的複雜度最少與g(n)一個數量級,即大於等於。
o符號,f(n) = o(g(n)),表示f(n)的複雜度要比g(n)的數量級小,即小於。
例如2n = o(n^2) ,但是2n^2 != o(n^2)- ω符號,f(n) = ω(g(n)),表示f(n)的複雜度要比g(n)的數量級大,即大於。
2.遞迴式
演算法設計中經常會用到遞迴,利用遞迴式的方法可以清晰地顯示演算法的整個過程,而對於分析演算法的複雜度,解遞迴式就有了用處。
1. 代換法
利用數學歸納法證明遞迴式的時間複雜度是否符合上界或下界。
例如 T(n)= 4T(n/2) +n , [T(1) = O(1)]
假設T(k) ≤ ck^3 (k<n) ,帶入上面遞迴式,得到
T(n) ≤ 4c(n/2)^3 + n = 1/2cn^3+n = cn^3-(1/2cn3-n)≤cn^3這樣就得到了一個上界O(n^3)。
假設T(k) ≤ ck^2 (k<n) ,帶入上面遞迴式,得到
T 因此這裡無法得到T(n) ≤cn^2,也就是說O(n^2)不是T(n)的上界。
2. 遞迴樹
在遞迴樹中,每一個結點都代表一個子代價,每層的代價是該層所有子代價的總和,總問題的代價就是所有層的代價總和。
所以,我們利用遞迴樹求解代價,需要知道,一個是每一層的代價,一個是樹的高度。
如下面的例子所示:

得最後的Θ(n)= n^2。
3.主定理方法
主定理方法的證明
如下圖所示,最後的葉節點數量為 a^(logbn) = n^(logba),因此O(n)的取值和f(n)以及葉節點數量有關。
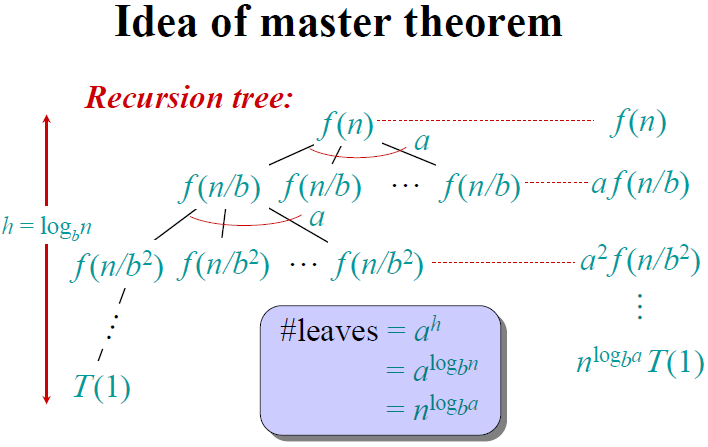
1,整個遞迴樹的權重從根節點到葉節點一直增加,所以整個遞迴樹的權重主要在葉子節點上;
2,(k = 0)遞迴樹每層的權重大致相同,總共h層,所以整個遞迴樹的權重將各層的權重加起來即可;
3,則與CASE 1的情況正好相反,所以整個遞迴樹的權重主要在根節點上。