一、神經網路是什麼？

目前最廣泛使用的定義是Kohonen於1988年的描述，神經網路是由具有適應性的簡單單元組成的廣泛並行互連的網路，它的組織能夠模擬生物神經系統對真實世界物體所做出的互動反應。

二、神經網路的組成

1、神經元模型

神經元模型，即上述定義中的簡單單元。

在生物神經網路中，每個神經元與其他神經元相連，當它興奮時，就會向相連的神經元傳送化學物質，從而改變這些神經元內的電位；如果某神經元的電位超過了一個閾值，那麼它就會啟用，即興奮起來。向其他神經元傳送化學物質。

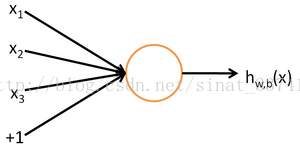
我們把上述的這種神經元模型抽象出來，這就是M-P神經元模型：

神經元接受輸入x，通過帶權重w的連線進行傳遞，將總輸入訊號與神經元的閾值進行比較，最後通過啟用函式處理確定是否啟用。

2、閾值

閾值，又稱為bias，其含義有點類似閥門。在計算中，可以將閾值看作一個固定輸入為-1的啞節點對應的連線權重。

3、啟用函式

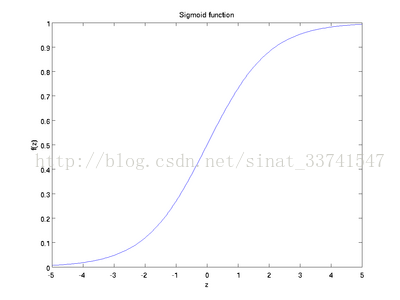
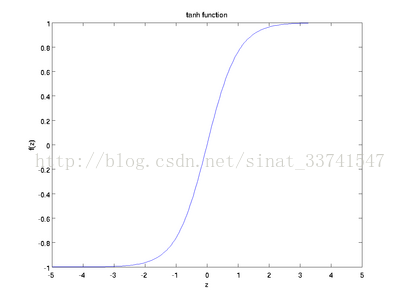
理想中的啟用函式是階躍函式，但實際使用中由於階躍函式不光滑，不連續，我們一般使用sigmoid或者tanh函式，如下：

兩者都是將較大範圍的輸入值擠壓到一個小範圍內，如(0，1)或者(-1, 1)，即上述的確定神經元是否啟用。

三、多層前饋神經網路

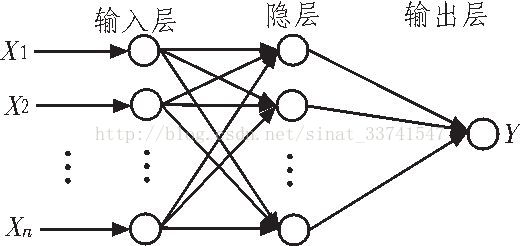
兩層神經元，即輸入層+輸出層(M-P神經元),構成感知機。而多層功能神經元相連構成多層前饋神經網路，輸入層與輸出層之間的一層神經元，稱為隱層：

如圖所示，每層神經元與下一層神經元互連，神經元之間不存在同層連線，也不存在跨層連結，這樣的結構稱多層前饋神經網路。

四、誤差逆傳播

神經網路學習的過程，其實就是根據訓練資料，來調整神經元之間的連線權w以及每個功能神經元閾值b的過程。

誤差逆傳播就是其中一種廣為人知的訓練方法，其核心的思想非常簡單，對於訓練資料(x，y)，若當前神經網路的輸出為Y，則神經網路的權重：

w = w + *w， 其中*w = n(y - Y)x

從上可以看出，假設訓練結果正確，則權重w不會發生改變；假如錯誤，則會對w進行一定調整，其中n為學習率，對學習速度有影響。多層神經網路從輸出層往輸入層逆方向傳播誤差進行權重調整，即所謂的誤差逆傳播演算法。

誤差逆傳播演算法基於梯度下降，這裡就不展開描述，詳細可以看我的另一篇部落格：梯度下降法

五、最優解

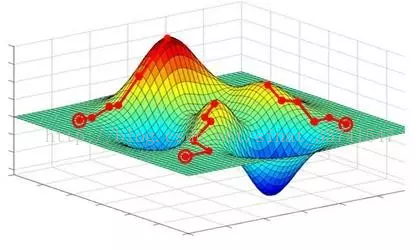
神經網路的訓練過程即是一個引數尋優過程，基於梯度下降求得的可能是區域性最優但不一定是全域性最優解：

所以實際調參過程中，往往需要多次試驗，才能得到一個較為滿意的模型。