題目描述
用N個三角形最多可以把平面分成幾個區域?

輸入
輸入資料的第一行是一個正整數T(1<=T<=10000),表示測試資料的數量.然後是T組測試資料,每組測試資料只包含一個正整數N(1<=N<=10000).

輸出
對於每組測試資料,請輸出題目中要求的結果.

樣例輸入
2
1
2

樣例輸出
2
8

一個三角形，把平面分割為兩部分，一個是內部，一個是外部。
n個三角形擺放位置可以重疊，我們來分析一下兩個三角形的情況，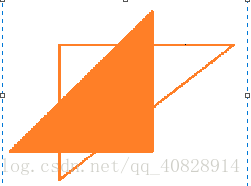
可見，共有八個部分，多出來的六個部分剛好就是交點的個數，一個線與三角形相交最多有兩個交點，每個三角形有三條邊，有兩個三角形時是用一個三角形分割另一個三角形，因此，交點個數：1*（3*2），當有一個三角形分割另兩個三角形時，2*（3*2），可以認為，那個（3*2）就是一個三角形分割另一個三角形時新產生的交點個數，因此f（n）=f（n-1）+（n-1）*6

#include<iostream>
using namespace std;
int main(){
    int n,a,i;
    cin>>n;
    while(n--){
        cin>>a;
        int b=2,c;
        if(a==1) cout<<2<<endl;
        else{
            for(i=2;i<=a;++i){
                c=b+6*(i-1);
                b=c;
            }   
            cout
 
<<c<<endl;
        }

    }
}