.偶數階幻方
說實話，偶數階幻方我一直以為只有一種，就是2*n階幻方問題。查了一下才知道偶數階幻方也分為兩小類。

①.4*n階幻方
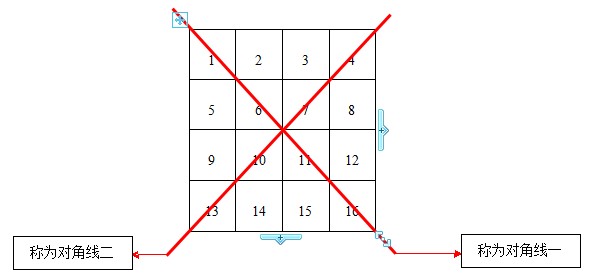
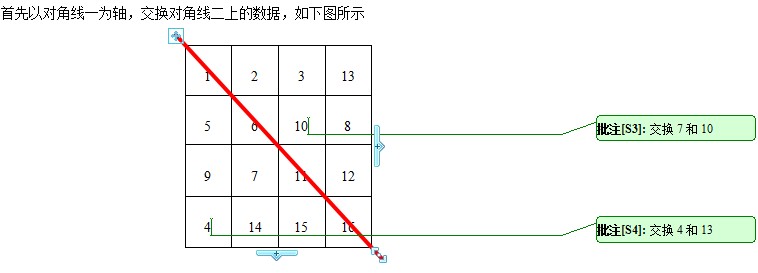
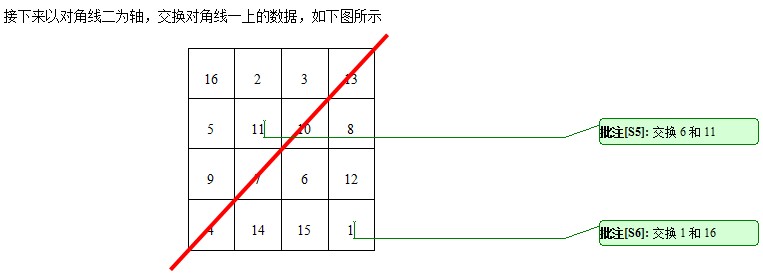
4*n階幻方的生成其實很簡單，即對方格中對角線上的資料，先以一條對角線（稱對角線一）為對稱軸，交換另一對角線（稱對角線二）的資料；然後以對角線二為對稱軸，交換對角線一的資料。說的直白一點，假設矩陣名為MagicSquare，就是交換MagicSquare[i,j]和MagicSquare[n-1-i,n-1-j]。老辦法，作圖來說明。圖如下

好了，4*n階幻方也完了，怎麼樣，簡單吧！自己動手試試吧。

②.4*n+2階幻方
4*n+2，乍一看就較4*n麻煩了，事實也是如此，不過它的思想也簡單。就是將4*n+2看做2*（2*n+1）,這樣一來就轉化成了四個2*n+1求幻方。
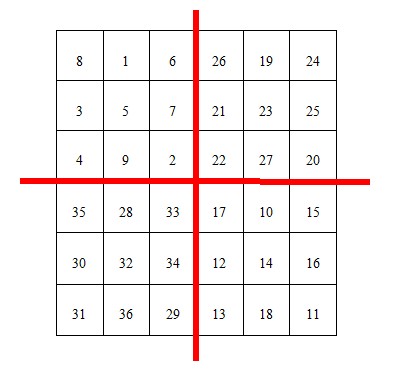
附註：下面的我以6階幻方為例，那麼，4*n+2=6，所以n=1。

我通過描述每個步驟加上圖形的方式來表述4*n+2階幻方實現的過程。

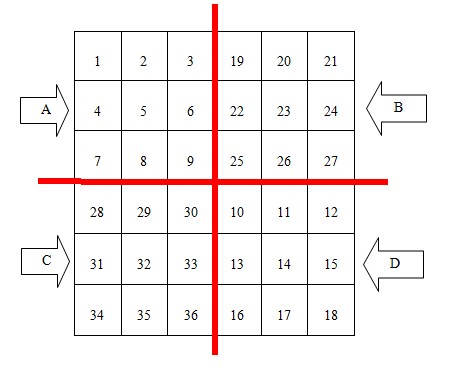
第一步：把整個表格分成4個（2*n+1）*（2*n+1）的小表格，分別叫A,B,C,D。見下圖

第二步：這樣A,B,C,D個小表格就成奇數幻方問題了。
①.將1，2，…，（2*n+1）*（2*n+1）這些數劃分給A，並對A實現奇數幻方;
②.將（2*n+1）（2*n+1）+1,…，2（2*n+1）*（2*n+1）這些數劃分給B，並對B實現奇數幻方；
③.將2*（2*n+1）（2*n+1）+1，…3（2*n+1）*（2*n+1）這些數劃分C，並對C實現奇數幻方；
④.將3*（2*n+1）（2*n+1）+1，…4

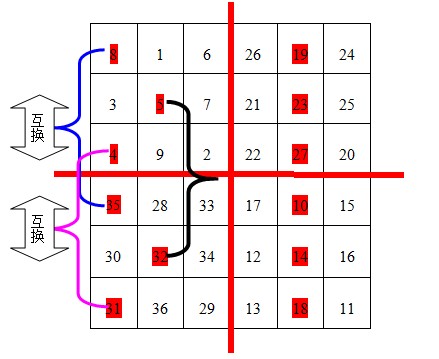
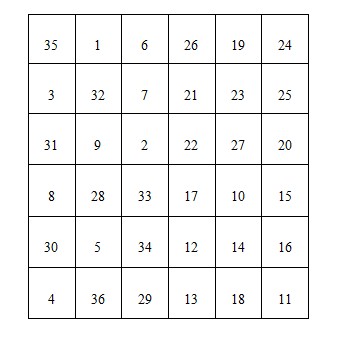
第三步：從A表中的中心（即第n行的MagicSquare[n][n]）開始，按照從左向右的方向，標出n個數，A表中的其他行則標出最左邊的n格中的數（在圖中用紅色背景標出）。並且將這些標出的數和C表中的對應位置互換。見下圖

第四步：在B表中的中心（如上解釋）開始，自右向左，標出n-1列，將B中標出的資料與D表中對應位置的資料交換。但是6階幻方中，n-1此時等於0，所以B與D不用做交換