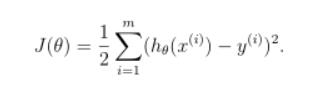第二課監督學習應用-梯度下降

阿新 • • 發佈：2019-02-18

課程概況：

線性迴歸、梯度下降、正規方程組

概述

汽車的自動駕駛：人類司機會為汽車提供一系列正確的行駛方向，之後嘗試更多正確的行駛方向，以確保汽車始終行駛在路上，就是汽車的任務了。-----監督學習中的迴歸問題：汽車嘗試預測表示行駛方向的連續變數的值。

舉例：房價預測

房價由多個因素，比如房子面積，臥室的數量等因素決定

監督學習的任務：學習房價與各因素之間的關係

引入符號：

m 表示訓練樣本的資料，也就是資料的行數 #training examples

x 表示輸入變數 #input variables 或 feature（特徵）

y 表示輸出變數 #output variables 或 target variable (目標變數)

(x y) 表示一個樣本

$\left ( x^{(i)},y^{(i)} \right )$ 第i個樣本訓練樣本列表中的第i行

n 表示特徵的數目

$\theta$ 學習演算法的引數，是學習演算法的任務

監督學習的過程

首先找到一個訓練集合（m個樣本），提供給學習演算法，得到一個輸出函式h，稱之為假設（hypothesis），這個假設可以對新資料x（不在訓練集中的）得到一個新的估計y，即假設h的作用是將輸入x對映到輸出y。

解決房價預測問題

1.對假設進行線性表示

$h(x)=h_{0}(x)=\theta _{0} + \theta _{1}x_{1}+ \theta _{2}x_{2}+...++ \theta _{i}x_{i}$

可將式子改寫為 $h(x)=\sum_{i=0}^{n}\theta _{i}x_{i}=\left [ \begin{matrix} \theta _{0}&\theta _{1} &...&\theta _{i}\end{matrix} \right ]\begin{bmatrix} x_{0}\\ x_{1} \\ ...\\x_{i} \end{bmatrix}=\theta ^{T}x$

2.嘗試讓學習演算法的預測值在訓練資料上儘可能準確

我們的目標即求解引數 $\theta$ ，選取的引數能使預測值和實際值的方差最小

目標函式：

其中 $h_{\theta }(x^{(i)})$ 表示每個樣本經過學習演算法得到的預測值。 $y^{(i)}$

代表每個樣本的真實值

目標： $min_{_{\theta }}J(\theta )$ ,求 $J(\theta )$ 的最小值

3.求最小值的演算法

3.1 搜尋演算法

基本思想：給定引數向量 $\theta$ 一個初始值（例如 $\theta =\vec{0}$ ），不斷改變引數向量的值，使得 $J(\theta )$ 不斷減小，直到 $J(\theta )$ 收斂為最小值

3.1.1 批梯度下降演算法

其中梯度下降演算法（Gradient Descent）是經典的一種搜尋演算法，其中心思想是尋找下降最大的梯度改變，從而最快收斂至最小值，就像一個人站在山上，環顧四周，尋找最快的下山方式。

$J(\theta )$ 的影象表示如圖所示：

一開始初始化一個向量作為初始值，假設該三維圖為一個三維地表。梯度下降的方法是，你環視一週，尋找下降最快的路徑，即為梯度的方向，每次下降一小步，再環視四周，繼續下降，以此類推。結果到達一個區域性最小值，如下圖：

特點：梯度下降的結果依賴於引數的初始值，初始值不同，可能會導致不同的結果。

$\theta$ 的更新方程為 $\theta _{i}:=\theta _{i}-\alpha \frac{\alpha }{\alpha \theta _{i}}J(\theta )$

每一次將減去對求偏導的結果，即沿最陡峭的“山坡”下降

更新方程的推導：（考慮只有一個訓練樣本）

代入更新方程中： $\theta _{i}:=\theta _{i}-\alpha(h_{\theta }(x)-y)x_{i}$

：學習速度，即決定你下山時每一步邁多大。設的過小，收斂時間長，設的過大，可能會超過最小值

考慮m個樣本數量的情況--批梯度下降演算法（batch gradient descent）

演算法流程:

重複更新 $\theta$ 的值直到演算法收斂 $\theta _{i}:=\theta _{i}-\alpha\sum_{j=1}^{m}(h_{\theta }(x^{(j)})-y^{(j)})x_{i}^{(j)}$

檢測是否收斂的方法：

1) 檢測兩次迭代的改變數，若不再變化，則判定收斂

2) 更常用的方法：檢驗，若不再變化，判定收斂

該演算法的缺點是：每一次更新的時候都需要遍歷整個訓練樣本，對m個訓練樣本進行求和，所以該演算法只適用於小樣本。

如果遇到樣本數量大的時候，我們將使用下面這個演算法

3.1.2隨機梯度下降演算法

也稱為增量梯度下降演算法

演算法流程如下：

Repeat 直到演算法收斂{

for j=1 to m {

$\theta _{_{i}}:=\theta _{_{i}}-\alpha (h_{\theta }(x^{(j)})-y^{(j)})x_{i}^{(j)}$ (更新所有的 $\theta_{i}$ )

}

該演算法的特點在於：每次更新只使用一個樣本資料，適用於樣本數量比較大的情況下。但是該演算法不會精確的收斂到全域性的最小值。

3.2 正規方程組

不再需要迭代的求 $\theta$

定義對函式 $J(\theta )$ 求導數的符號：

一些關於跡運算子和導數的定理：

如果A是方陣，那麼

定義矩陣X，稱為設計矩陣，包含了訓練集中所有輸入的矩陣，第i行為第i組輸入資料，即：

那麼 $X\theta =\begin{bmatrix} x^{(1)T }\theta\\ ... \\ x^{(m)T }\theta \end{bmatrix}=\begin{bmatrix} h_{\theta }(x^{(1)})\\ ... \\ h_{\theta }(x^{(m)}) \end{bmatrix}$

將真實值 $\vec{y}$ 定義為 $\vec{y}=\begin{bmatrix} y^{(1)}\\ ... \\ y^{(m)} \end{bmatrix}$

那麼 $x\theta -y=\begin{bmatrix} h_{\theta }(x^{(1)})-y^{(1)}\\ ... \\ h_{\theta }(x^{(m)})-y^{(m)} \end{bmatrix}$

對目標函式求偏導：