AVR121-使用過取樣增加ADC精度
1. 介紹
在大多數情況10位精度已經足夠了,但是某些情況下需要更高的精度。特殊的訊號處理技術可以用來提高測量的精度。使用一種稱為“過取樣和抽取”的方法可以得到較高的精度,不需要使用外部的ADC。
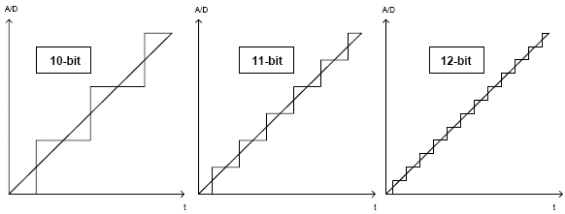
Figure 1-1. 增加解析度
2. 操作理論
ADC的參考電壓和ADC的精度決定了ADC的步距。ADC的參考電壓VREF可以選擇使用AVCC,內部的2.56V / 1.1V參考電壓,或者AREF引腳上的電壓。較低的VREF提供了較高的電壓精度但是同時減少了輸入訊號的動態範圍。如果2.56V的VREF被選擇,它將給使用者大約2.5mV的轉換精度,並且最高的輸入電壓是2.56V。選擇使用ADC輸入通道的增益,這使使用者有更好的精度來測量模擬訊號,代價是損失ADC的動態範圍。如果不能接受以動態範圍交換精度,可以採用過取樣來增加精度。這個方法受到ADC的特性限制:使用過取樣和抽取將降低ADC的量化誤差,但是不能減少ADC的非線性化誤差。
2.1 取樣頻率
Nyquist定理規定訊號的取樣頻率必需至少是訊號頻率的兩倍,否則高頻部分將有損失(帶通)。最小需要的取樣頻率稱為Nyquist 頻率。
公式 2-1. Nyquist 頻率
這裡
取樣頻率是CPU時鐘的分頻的結果,一個較低的分頻係數給出較高的ADC時鐘頻率。在一個特定點,較高的ADC時鐘將降低轉換的精度,即有效資料位ENOB(Effective Number Of Bits)。 所有的ADC都有頻寬限制, AVR的ADC也不例外,按照資料手冊的說法,要獲得10位轉換精度,ADC時鐘頻率大概在50kHz –200kHz。當ADC時鐘是200kHz時,取樣頻率大約是15kSPS(次每秒),可以取樣訊號的上限大約是~7.5kHz。按照資料手冊,ADC時鐘最高可以到1Mhz,
儘管這將降低ENOB。
3. 理論
3.1 過取樣和抽取
過取樣和抽取理論的背後是非常複雜的,但是的方法卻是比較容易的。這個技術要求大量的取樣,這些額外的取樣完成訊號過取樣。每增加額外的一位精度,訊號必需過取樣4倍。頻率和輸入訊號的關係在公式3-1中。為了儘可能最好的重現訊號,這麼多次的取樣是必需的,因為大量的取樣平均後可以更好的重現輸入訊號。這可以認為是這篇應用筆記的主要內容,下面的理論和例子用來進一步解釋。
公式 3-1. 過取樣頻率
3.2 噪聲
為了使這個方法正常工作,訊號成分在轉換過程中不能發生變化。但是成功增加精度的另一個標準是輸入訊號在取樣時有所變化。這看起來是矛盾的,因為訊號的變化意味著較少有效的 LSB,變化的訊號可以看成是訊號的噪聲成分。在訊號過取樣時,噪聲使訊號產生微小的變化。ADC的量化誤差一般至少是0.5LSB,因此噪聲幅度超過0.5 LSB就改變了LSB。噪聲幅度有1-2LSB時更好,因為可以保證幾次取樣不會總是相同的值。
使用抽取技術時,噪聲的標準:
- 訊號成分在轉換時不能變化。
- 訊號上有一定的噪聲。
- 噪聲的幅度至少有1 LSB。
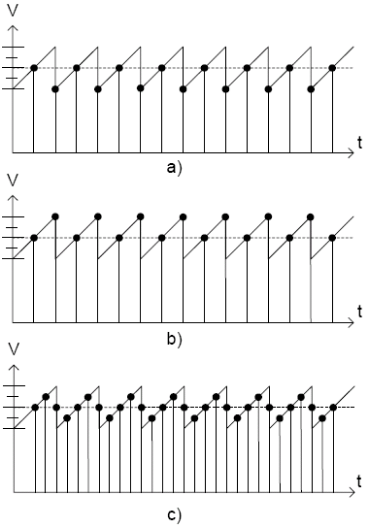
通常AD轉換時有一定的噪聲,噪聲可能是熱噪聲、CPU的核心產生的噪聲、I/O埠切換帶來的噪聲、電源變化引起的噪聲(特別是開關電源)等等。這些噪聲在大多數情況下可以使這個方法正常工作了,但是在特殊情況下,需要引入噪聲到輸入訊號,這個方法叫抖動。圖 3-1 (a)展示了測量電壓訊號的在兩檔之間時,簡單將4次取樣結果平均沒有太大作用,結果可能是同樣的數字,它只能消除訊號的波動。圖3-1 (b) 顯示新增人工噪聲到輸入訊號後,改變了轉換結果的LSB。新增4次取樣同樣的取樣步驟,產生的結果給出更好的精度,如圖3-1 (c) 所示,ADC的“虛擬精度”從10位增加到11位。這個方法就是抽取,在3-3小節會進一步講解。
圖 3-1. 精度從10位增加11位
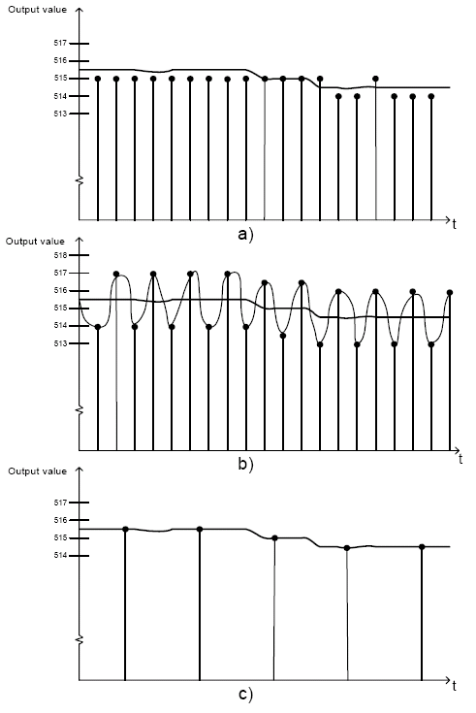
另外使用這個方法的理由是可以增加信噪比,提高有效位數ENOB,並將噪聲平展開來,使噪聲對每個二進位制數的影響減少。雙倍的取樣頻率將減少帶內噪聲3dB,增加有效測量精度0.5位。
3.3 平均
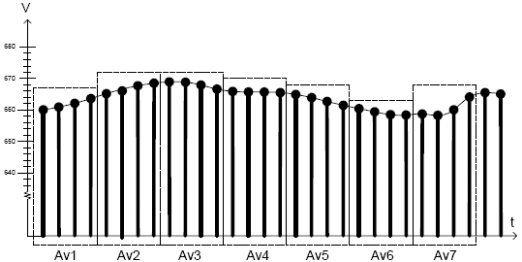
一般平均就是取樣M次,結果之和再除以M。正常平均時,ADC測量的資料等效於通過了一個低通濾波器,減弱了訊號的波動噪聲,並使峰值平緩。滑動平均法經常用來這樣做,讀取M次,將結果放到一個迴圈佇列,平均最近M次的結果。它有輕微的延時,因為每次的結果都是最後M次取樣的結果。資料視窗可以重疊也可以不重疊,圖 3.2 顯示了 7個(Av1-Av7) 獨立的不重疊滑動平均的結果。
圖 3-2. 滑動平均原理
要注意普通平均不會增加轉換的精度,抽樣或插值方法和過取樣一起使用,才能增加精度。數字訊號處理過取樣和訊號低通濾波經常看成是插值。這時,插值用來產生在大量取樣後的新取樣結果。越多的平均取樣數,越容易選擇低通濾波,插值結果越好。額外的M次取樣,象普通平均那樣累加起來,但是結果不象普通平均那樣除以M。而是結果右移N(N是希望增加的額外精度),從而比例化成正確的結果。右移一個二進位制數一次等於除以2。如公式3-1,精度從10位增加到12位需要總共16次10位的取樣。這16次10位結果產生一個14位計算結果,其中最後兩位是無用的,右移後成為12位結果。比例係數sf在公式3-2給出,它是總共4n次取樣後的除數,這樣才能得到正確的比例化結果。n是需要的額外精度。
公式 3-2.
3.4 過取樣和抽取什麼時候工作
正常情況下訊號包含了一定的噪聲,這個噪聲通常具有高斯噪聲的特性,更常用的名稱是白噪聲或熱噪聲,在寬頻譜中總能量均勻分佈在整個頻段範圍。在這些情況下,如果噪聲的幅度可以改變ADC的LSB,‘過取樣和抽取’的方法就能夠工作。
在其他情況,就有必要引入人工的噪聲到輸入訊號中,這個方法叫做抖動。這個噪聲波形應當是高斯噪聲,不過週期性的噪聲也可以。噪聲訊號的頻率和取樣頻率有關,一個原則是:“當新增N次取樣時,噪聲週期不能超過N次取樣的週期”。噪聲的幅度至少需要1LSB。.當新增人工噪聲時,需要記住噪聲的值是0;不充分的過取樣會產生偏差,如圖3-3.
圖 3-3. 不充分取樣造成的偏差
虛線是鋸齒波訊號的平均值,圖3-3 (a)將引起負偏差,圖3-3 (b) 引起正偏差,圖3-3(c)的取樣是充分的,就避免了偏差。為了產生人工噪聲訊號,可以使用AVR微控制器的計數器。因為計數器和ADC使用了相同的時鐘源,這就能使噪聲和取樣頻率同步,避免了偏差。
3.5 例子1
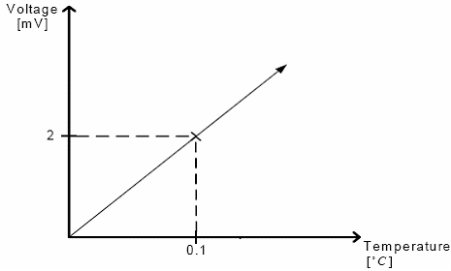
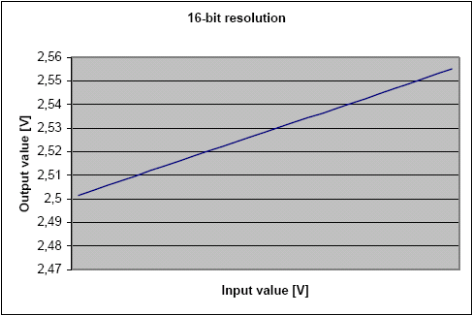
一個都柏林的釀酒師想測量釀酒時的溫度。一個緩慢變化的訊號表示了溫度,在這種環境下一 般溫度對應的電壓是2.5 V。圖3-4顯示了溫度測量裝置的特性。
圖 3-4. 電壓 / 溫度函式
釀酒師不希望縮小輸入訊號的範圍,選擇5V作為ADC的基準。這時10位ADC不能提供足夠精度的轉換結果,因為結果的LSB大約是5mV的‘步距’。這個結果會引起0.25°C的誤差,所以不能被接受。釀酒師希望結果有0.1°C的精度,要求電壓的解析度小於2mV。如果測量使用了12位的ADC,那麼電壓步距的LSB將減小到約1.22mV。釀酒師需要的是用10位ADC產生虛擬12位ADC結果。輸入訊號是緩慢變化的,不需要很高的取樣頻率。按照資料手冊,ADC時鐘頻率在50kHz到200kHz之間可以保證10位精度,釀酒師因此選擇了50kHz的ADC時鐘頻率。取樣頻率變為約3800次/秒。一個溫度下測量出直流引數是2.4729V,表 3-1 顯示了不同解析度選項下測量的這個引數,Vin = 2.4729V 而 VREF = 5V。
Table 3-1. 解析度選項
| 解析度 | 電壓解析度 | 過取樣 | 右移 | 理想抽取結果 | 理想電壓 | 最大頻寬 |
|---|---|---|---|---|---|---|
| 10 | ~5 mV | NA | NA | NA | 2.4658V | ~7600Hz |
| 11 | ~2.5 mV | 4X | 1X | 1012 | 2.4707V | ~1900Hz |
| 12 | ~1.22mV | 16X | 2X | 2025 | 2.4719V | ~475Hz |
| 13 | ~610 uV | 64X | 3X | 4051 | 2.4725V | ~118Hz |
| 14 | ~300 uV | 256X | 4X | 8103 | 2.4728V | ~29Hz |
| 15 | ~150 uV | 1024X | 5X | 16206 | 2.4728V | ~7Hz |
| 16 | ~75 uV | 4096X | 6X | 32413 | 2.4729V | ~3Hz |
注:1. ADC 時鐘 = 200kHz
這個結果單次轉換結果是505,初略看上去結果是正確的,但是這個二進位制數字相當於2.4683V, 這使使用者不確定溫度測量的誤差,在某些情況下可能是危險的。如前面推斷的,訊號通常包含了足夠的噪聲來使用抽取法。
為了增加1位精度,新增4次相鄰的取樣,這些取樣出的值相互之間因為有噪聲存在所以有微小的不同。新增4次取樣:508 + 507 + 505 + 505 = 2025。按照抽取原則,增加n位精度,就需要右移n次。結果右移1位,最後移位後結果是1012。同樣,訊號充分過取樣可以進一步提高精度, 達到12位。新增16次10位取樣並右移2位結果就能達到,結果是2025。這個數字更可信,因為使用12位結果時誤差已經減少到約1.22mV。這個例子顯示了使用者起初取樣一個緩慢變化訊號, 取樣速度是3800次每秒,電壓精度約5mV。現在取樣速度是240次每秒,12位精度,電壓精度 約1.22mV。
使用者可以按慣例平均16次12位取樣結果以消除波動,這就是把16次取樣結果加起來在除以16,終端使用者得到的是15 SPS 的12位取樣。(15 * 16 * 16 = 3840)
- 普通平均將減少隨機噪聲
- 過取樣和抽取將利用噪聲增加精度
3.6 例子2
為了展示這個方法,下面的例子將顯示怎樣不需要使用外部的ADC獲取更高的精度。一個訊號發生器用來產生0V到5V的線性斜坡訊號。在一個‘低噪聲’環境下,一個訊號發生器和一個AVR微控制器連線到STK500開發板,這可能沒有足夠大的噪聲來影響10位的訊號。這就需要引入人工噪聲訊號到輸入的訊號。有4種方法被成功使用:
- 新增訊號發生器產生的噪聲,直接連到輸入訊號。
- 使用AVR的PWM產生噪聲。
- 當使用AVCC作為VREF時,使用AVR產生的噪聲新增到AREF。
- 當使用AREF作為VREF時,新增AVR產生的噪聲到AREF。
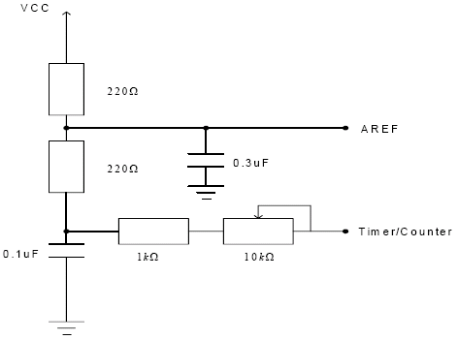
最容易的方法是直接新增白噪聲到訊號,但在大多數情況使用者沒有或者不希望有這種噪聲。一個更可行的方法是使用AVR微控制器產生一個PWM訊號,然後低通濾波這個‘噪聲’成直流,並且紋波的峰值達到LSB,一個這樣的例子在圖 3-5中展示。
圖3-5. LP-濾波
如果VCC = 5V,濾波的訊號在 AREF 引腳有2.5V,當計數器的佔空比是0%時;當佔空比是100%就是5V。在這個例子,佔空比是50%,基本頻率大約是3900Hz,10kΩ的電位器用來調節紋波。PWM訊號即作為ADC的參考電壓,也作為噪聲發生器(AVCC作為ADC的參考電壓)。這個方法認為參考電壓的微小變化和輸入訊號的微小變化結果是相同的,這就不用幹擾輸入訊號了。
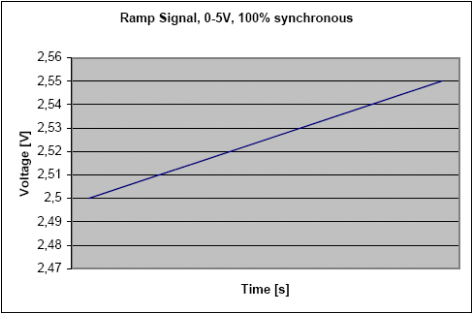
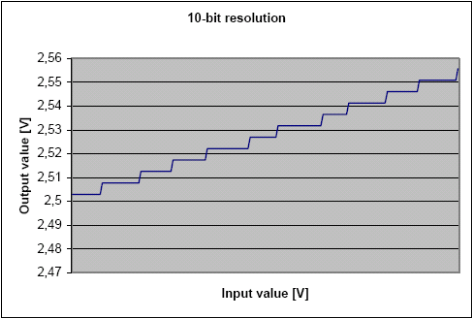
圖 3-6顯示測量線性斜坡訊號。圖3-7顯示10位離散化的輸入斜坡訊號,測量沒有新增人工噪聲, 量化步距是很明顯的。為了增加精度,就要減少量化步距。
圖3-6. 斜坡訊號0-5V, 100% 同步
圖3-7. 10位精度量化的訊號
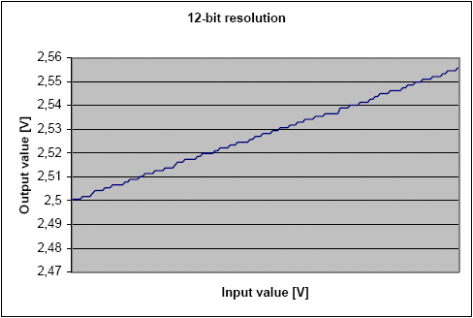
圖3-8顯示出輸入訊號12位離散化結果(AREF作為ADC的參考電壓,AREF添加了噪聲)。按照 公式3-1,每12位結果需要16次10位取樣。ADC偏差調整和應用筆記AVR120一致,增益誤差也需要調整。
圖3-8. 12位精度量化
圖3-9顯示14位離散化結果,圖3-10顯示16位的結果。當測量訊號包含噪聲,或者參考電壓象這個例子的,要注意頂端和底端的值要減去噪聲訊號的幅度,稍微減少了測量訊號的動態範圍。在某些情況下,作為安全邊界,偏差是100mV。
圖3-9. 14位精度量化的訊號
你可以清楚地看到過取樣和抽取法顯著增加了精度。
總結
當ADC取樣一個訊號時,不連續的量化訊號會引入一些誤差,通常稱為量化誤差。一般平均的只能消除訊號的波動,但抽取法可以提高精度。對一個4倍過取樣的訊號,4個相鄰的資料點平均產生一個新的資料點。過取樣頻率的計算參考公式3-1。新增額外的取樣並右移結果係數n,產生提高n位精度的結果。平均4次ADC取樣的結果獲得新ADC的結果是同樣ADC取樣速率的¼,但是同時平均了量化噪聲,改善了SNR,這將增加ENOB並減少量化誤差。快速的ADC和低記憶體消耗,使得過取樣的優點是顯著的。
- 增加一些噪聲到訊號,至少 1 LSB。
- 如果噪聲的幅度不夠,新增噪聲到訊號。
- 累計
4n 次10位取樣,這裡 n 是希望得到的額外精度。 - 右移n次,比例累計的結果。
- 按照應用筆記AVR120補償誤差。