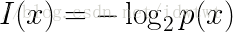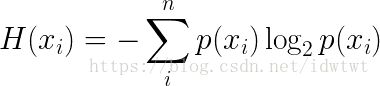1 資訊量

資訊量即資訊多少的度量。跟我們認識中秒是時間多少的度量，米是長度多少的量度是一樣的意思。

百度百科上定義秒：銫133原子基態的兩個超精細能階之間躍遷時所輻射的電磁波的週期的9,192,631,770倍 的時間 。

那資訊的多少怎麼衡量呢？一個人告訴你一件事，比如太陽從東方升起；你說這是常識啊，大家都知道。一個人告訴你，明天某個時間在某個地方待著，將有一個億支票掉下來，這個事情概率比較低，資訊量非常大,知道了這個事情價值非常大。感性上我們可以理解資訊量為給我帶來價值的多少（給你帶來多少價值，對等的就是要付出多少代價，似乎有點繞）。實質工程中，資訊量的引入是與資訊的傳輸和儲存相關的。舉個例子：

世界盃比賽，假如最後剩下巴西，法國，比利時，英格蘭，巴西得冠軍的概率1/2,法國得冠軍的概率1/4,比利時得冠軍的概率1/8，英格蘭冠軍概率1/8（非球迷，錯了勿怪）。我們要設計協議，傳輸某個隊伍得了冠軍的資訊。如何設計呢？有人說簡單，用兩個位元：

00：巴西隊得冠軍

01：法國隊得冠軍

10：比利時得冠軍

11：英格蘭得冠軍

但是這樣設計合理嗎?無論哪個隊得冠軍，我們都得傳輸2個位元。我們前面知道了各個隊得冠軍的概率，如果這樣設計

1：巴西隊得冠軍

0：法國隊得冠軍

01：比利時得冠軍

11：英格蘭得冠軍

因為巴西隊和法國隊得冠軍的概率比較大，大概率我們只需傳輸一個位元就行了。基於這樣的設計，概率越小我們需要傳輸的位元位越多。如果以位元位的多少來衡量資訊量的多少，也就是概率越低資訊量越大。

基於此，給出資訊量的一個量化公式：

即如果信源的概率越大，該信源攜帶的資訊量越小（傳輸儲存代價越小）；信源概率越小，該信源攜帶的資訊越大（傳輸儲存代價越大）。

2 資訊熵

我們直接給出公式定義：

從公式中我們可以知道資訊熵其實是系統（信源系統）資訊量的期望。但是這個期望代表了一個系統的不確定性，資訊熵越大，不確定性越大。如何理解呢？我們基於資訊傳輸代價來理解，其實就是如果信源產生一個資訊，我們要傳輸這個資訊需要花費代價的最小平均位元位數。