今天是5月14日，我們按照規定，給出幾道答案等於14的題目。

（一）

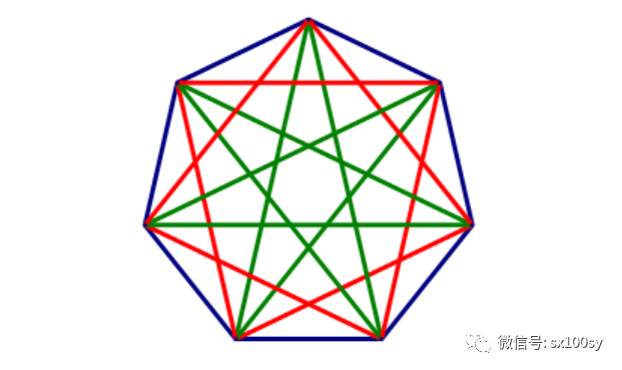
一個正七邊形有多少條對角線？（7個點之間兩兩連線，可以連接出7*6/2=21條線段，其中有七條是正七邊形的邊，那麼，剩餘線段的數量就是正七邊形對角線的數量，請您自己計算。另外，也可以從另一角度來計算對角線的數量：廣義的正七邊形還包括星狀七邊形。星狀七邊形有兩種，一種是從任意一個頂點出發，相隔一個頂點依次進行連線，這樣，連線七次後，回到出發點，形成下圖中紅色的星狀七邊形。第二種也是從任意一個頂點出發，但這次是相隔兩個頂點依次進行連線，於是，也是連線七次後回到出發點，連接出下圖中綠色星狀七邊形。紅綠兩種星狀七邊形是不同的，互相不會重複或重疊。兩種星狀七邊形的邊合在一起，構成全部正七邊形的對角線。）

（二）

一個正四邊形（正方形）可以有兩種方法把它劃分成兩個三角形：

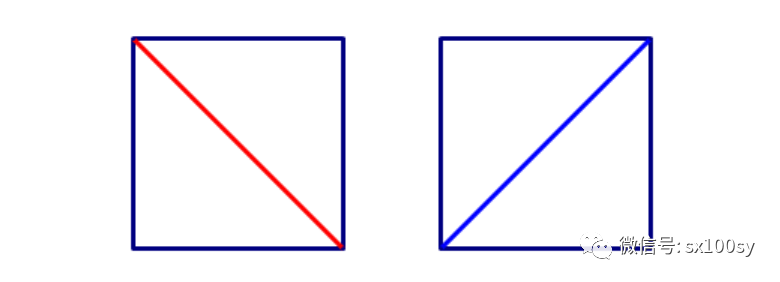
一個正五邊形有下面五種方法把它劃分成三角形：

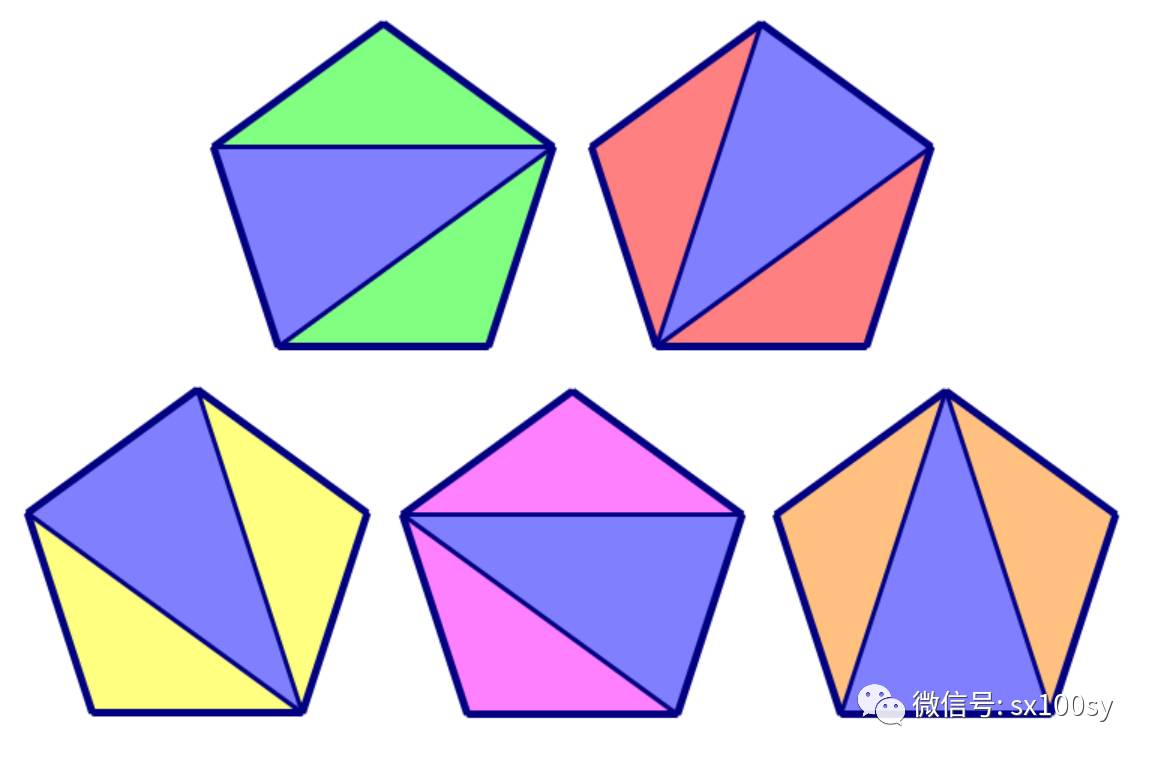
那麼，一個正六邊形可以有多少種方法把它劃分成三角形呢？

下面是幾個公式：

（1）尤拉給出的公式（n代表正多邊形的邊數）：

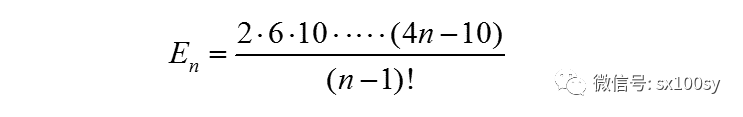
（2）塞格納（Johann Andreas Segner）的公式（其中規定E2=1）：

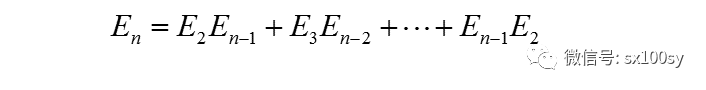
請您自行驗證一下正六邊形內劃分出三角形的方法共有多少種（n取6時）。上面是對正多邊形進行的討論。其實對凸多邊形都是成立的。