排列樹問題

給定無向連通圖G和m種不同的顏色。用這些顏色為圖G的各頂點著色，每個頂點著一種顏色，是否有一種著色法使G中任意相鄰的2個頂點著不同顏色?

輸出結果：

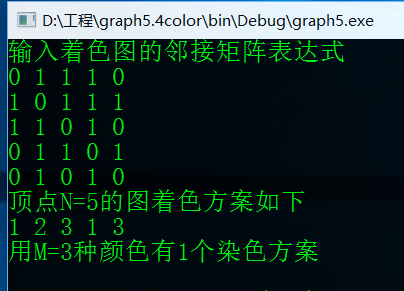
#include <iostream>

using namespace std;

const int N=5;   //
const int M=3;

//5.8節圖的m著色問題（回溯法）


/*
0 1 1 1 0
1 0 1 1 1
1 1 0 1 0
0 1 1 0 1
0 1 0 1 0

              頂點N=5的圖鄰接矩陣如上。。。
*/

class Color{
     friend int mColoring(int ,int ,int **);
     private:
              bool Ok(int k);             //用於判斷某一頂點染色x[k]能否為某一值 i ;
              void Backtrack(int t);

              int n,        //圖的頂點數
                  m,        //可用顏色數
                  **a,      //圖的鄰接矩陣
                  *x;      //當前解
              long  sum;    // 當m為某一確定值時，當前找到的m著色方案數
};


bool Color::Ok(int k){      //檢測當前頂點染色x[k]為值 i 能否滿足

              for(int j=1;j<=n;j++){
                            if( (a[k][j]==1) &&(x[j]==x[k])  )//相鄰且顏色相同，則
                            return false;                     //返回false
              }
              return true;

}


void Color::Backtrack(int t){
              if(t>n){
                            sum++;
                              cout<<"頂點N="<<N<<"的圖著色方案如下"<<endl;
                            for(int i=1;i<=n;i++)

                            cout<<x[i]<<" ";
                            cout<<endl;
              }
              else

                for(int i=1;i<=m;i++){
                            x[t]=i;
                            if(Ok(t)) Backtrack(t+1);
                           //x[t]=0;
              }



}



int mColoring(int n,int m,int * * a){

              Color X;
              X.n=n;
              X.m=m;
              X.a=a;
              X.sum=0;
              int  *p=new int [n+1];
              for(int i=0;i<=n;i++){
                            p[i]=0;
              }
              X.x=p;
              X.Backtrack(1);
              delete []p;
              return X.sum;



}
int main()
{

cout<<"輸入著色圖的鄰接矩陣表示式"<<endl;

  int **a = new int *[N+1];
    for(int i=1;i<=N;i++)
    {
        a[i] = new int[N+1];
    }
    for(int i=1;i<=N;i++)
     {
                   for(int j=1;j<=N;j++)
                    {
                       cin>>a[i][j];
                    }
     }


         int ans=mColoring(N,M,a);
     cout<<"用M="<<M<<"種顏色有"<<ans<<"個染色方案"<<endl;

    return 0;
}