問題描述:

圖的m-著色判定問題:  給定無向連通圖G和m種不同的顏色。用這些顏色為圖G的各頂點著色，每個頂點著一種顏色，是否有一種著色法使G中任意相鄰的2個頂點著不同顏色。

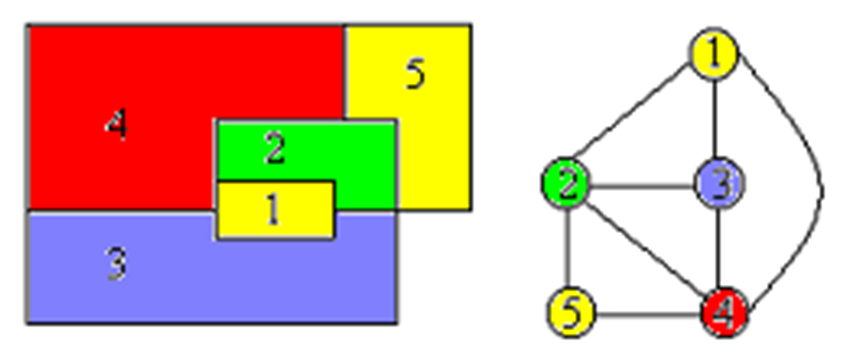
問題模型(圖來自網路):  (PS: 頂點的排列情況圖就省略了2333333。。。。 )

解決思路:  m圖中要使兩頂點間著色不同，即保證它們在不同列。這裡用二維陣列模擬各頂點的著色情況 (a[i][j]表示頂點i著第j號色)。約束函式為:

int place(int k){
    for(int i = 1;i<k;i++){     
        if(x[i]==x[k]){            //不能與已經著色的邊進行同色處理
            return 0;
        }
    } 
    return 1;
}
 

每一個頂點原則上有m種著色。但當前面頂點著色已確定，後面的節點著色必須符合約束函式。當回溯到葉子節點(t>n)時，排列情況數+1。然後再往上回溯。依次得出所有的排列情況。

程式碼 ：

/**
   @回溯法-m圖著色問題
*/
#include<iostream>
#include<algorithm>
#define MAX 100
using namespace std;
int n;             //圖的頂點數
int m;            //顏色數量
int x[MAX];      //記錄頂點的著色情況
long sum = 0;
int place(int k){
    for(int i = 1;i<k;i++){     
        if(x[i]==x[k]){                      //不能與已經著色的頂點進行同色處理
            return 0;
        }
    } 
    return 1;
}
void backpack(int t){
    if(t>n){
       sum++;
       cout<<"排列"<<sum<<"為:"<<endl;
       int a[MAX][MAX ] = {0};      
       for(int i = 1;i<=m;i++)  a[i][x[i]] = x[i];
       for(int i = 1;i<=n;i++){             //0表示未著色處理
           for(int j = 1;j<=m;j++){  
               cout<<a[i][j]<<" ";
           }
           cout<<endl;
       }
       //x[t] = -1;  //將最後一個節點置為-1,表示未探索過,防止回溯時產生影響。
    }else{
         for(int i = 1;i<=m;i++){          //頂點的著色處理
            x[t] = i;
            if(place(t)){                 
                backpack(t+1);   
            }else{
                 ;
            }
         }
    }
}
int main(){
    cout<<"輸入圖頂點與顏色數量:"<<endl;
    cin>>n>>m;
    backpack(1);
    cout<<"共有"<<sum<<"種著色方法"<<endl;
}