題面

傳送門

分析

對於每一個數a[i]，找到它後面第一個大於它的數a[p]，由p向i連邊，最終我們就會得到一個森林，且p是i的父親。為了方便操作，我們再增加一個虛擬節點n+1，把森林變成樹。

由於序列不是遞增的，不能二分。維護一個單調棧，棧頂元素最小。從n到1依次對每個 數操作，彈出棧裏比它小的數。如果棧為空，說明該數是森林中的根節點，向n+1連邊。否則棧頂元素就是第一個大於它的數，向它的編號連邊即可。

我們發現，對於每個查詢區間內的所有數，它對應著樹上的某些節點，記為標記節點。如果把標記節點之間的非標記節點去掉，我們就會得到一棵新樹，新樹上從某個節點到根的一條路徑對應著一個滿足條件的序列，則最大序列長度等於新樹上從葉子節點到根的最長路徑。這樣，我們就把問題轉化為了樹上的最長路徑。

顯然不能對每一個詢問建一棵新樹。我們發現新樹上的路徑長度就是原樹上的路徑經過的標記節點個數，如圖(加粗的節點為標記節點）。

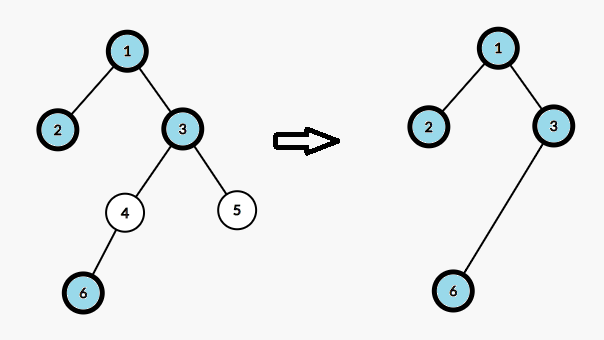
所以，我們建立一棵線段樹，線段樹的葉子節點存儲原樹上每個節點到根的路徑上的標記節點個數，線段樹維護最大值。

我們枚舉每個長度為k的區間[i,i+k-1],顯然從前一個區間轉移到當前區間時，只會增加一個標記節點，減少一個標記節點。每增加一個標記節點i，我們就將i的子樹內的所有節點的值+1，否則-1。答案即為整顆線段樹的最大值

時間復雜度\(O(n\log n)\)

代碼

#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#include<stack>
#include<algorithm>
#define maxn 1000005
using namespace std;
int n,k;
int a[maxn]; 
struct edge{
    int from;
    int to;
    int next;
}E[maxn<<1];
int head[maxn];
int sz=1;
void add_edge(int u,int v){
    sz++;
    E[sz].from=u;
    E[sz].to=v;
    E[sz].next=head[u];
    head[u]=sz;
}
int cnt=0;
int lb[maxn],rb[maxn];
void dfs(int x,int fa){
    lb[x]=++cnt;
    for(int i=head[x];i;i=E[i].next){
        int y=E[i].to;
        if(y!=fa){
            dfs(y,x);
        }
    }
    rb[x]=cnt;
}

struct node{
    int l;
    int r;
    int v;
    int mark;
}tree[maxn<<2];
void push_up(int pos){
    tree[pos].v=max(tree[pos<<1].v,tree[pos<<1|1].v);
}
void build(int l,int r,int pos){
    tree[pos].l=l;
    tree[pos].r=r;
    if(l==r){
        return;
    }
    int mid=(l+r)>>1;
    build(l,mid,pos<<1);
    build(mid+1,r,pos<<1|1);
    push_up(pos);
}
void push_down(int pos){
    if(tree[pos].mark){
        tree[pos<<1].v+=tree[pos].mark;
        tree[pos<<1].mark+=tree[pos].mark;
        tree[pos<<1|1].v+=tree[pos].mark;
        tree[pos<<1|1].mark+=tree[pos].mark;
        tree[pos].mark=0;
    }
}
void update(int L,int R,int v,int pos){
    if(L<=tree[pos].l&&R>=tree[pos].r){
        tree[pos].v+=v;
        tree[pos].mark+=v;
        return;
    }
    push_down(pos);
    int mid=(tree[pos].l+tree[pos].r)>>1;
    if(L<=mid) update(L,R,v,pos<<1);
    if(R>mid) update(L,R,v,pos<<1|1);
    push_up(pos); 
}
int query(int L,int R,int pos){
    if(L<=tree[pos].l&&R>=tree[pos].r){
        return tree[pos].v;
    }
    push_down(pos);
    int mid=(tree[pos].l+tree[pos].r)>>1;
    int ans=0;
    if(L<=mid) ans=max(ans,query(L,R,pos<<1));
    if(R>mid) ans=max(ans,query(L,R,pos<<1|1));
    return ans;
}

int nex[maxn];
void init(){
    stack<int>s;
    for(int i=n;i>=1;i--){
        while(!s.empty()&&a[s.top()]<=a[i]) s.pop();
        if(!s.empty()){
            int p=s.top();
            add_edge(p,i);
            add_edge(i,p);
        }else{
            add_edge(n+1,i);
            add_edge(i,n+1);
        }
        s.push(i);
    }
    dfs(n+1,0);
}
int main(){
    scanf("%d %d",&n,&k);
    for(int i=1;i<=n;i++){
        scanf("%d",&a[i]);
    }
    init();
    build(1,n+1,1);
    for(int i=1;i<=k;i++){
        update(lb[i],rb[i],1,1);
    }
    for(int i=1;i+k-1<=n;i++){
        int r=i+k-1;
        printf("%d ",query(1,n+1,1));
        update(lb[i],rb[i],-1,1);
        update(lb[r+1],rb[r+1],1,1);
    }
}
 

Codeforces 1132G(dfs序+線段樹)