A plane is flying at a constant height of hh meters above the ground surface. Let‘s consider that it is flying from the point (−109,h)(−109,h) to the point (109,h)(109,h) parallel with OxOx axis.

A glider is inside the plane, ready to start his flight at any moment (for the sake of simplicity let‘s consider that he may start only when the plane‘s coordinates are integers). After jumping from the plane, he will fly in the same direction as the plane, parallel to

There are ascending air flows on certain segments, each such segment is characterized by two numbers x1x1 and x2x2 (x1<x2x1<x2 ) representing its endpoints. No two segments share any common points. When the glider is inside one of such segments, he doesn‘t descend, so his second coordinate stays the same each second. The glider still flies along

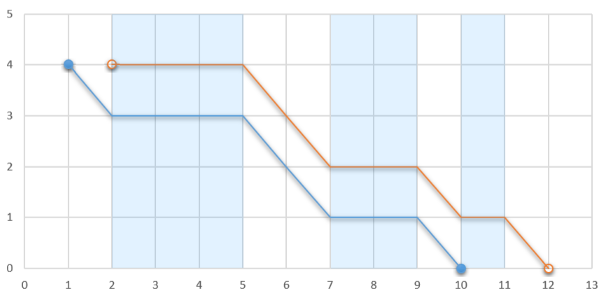
If the glider jumps out at 1 , he will stop at 10 . Otherwise, if he jumps out at 2 , he will stop at 12 .

Determine the maximum distance along Ox axis from the point where the glider‘s flight starts to the point where his flight ends if the glider can choose any integer coordinate to jump from the plane and start his flight. After touching the ground the glider stops altogether, so he cannot glide through an ascending airflow segment if his second coordinate is

The first line contains two integers nn and hh (1≤n≤2⋅105,1≤h≤109)(1≤n≤2⋅105,1≤h≤109) — the number of ascending air flow segments and the altitude at which the plane is flying, respectively.

Each of the next nn lines contains two integers xi1xi1 and xi2xi2 (1≤xi1<xi2≤109)(1≤xi1<xi2≤109) — the endpoints of the ii -th ascending air flow segment. No two segments intersect, and they are given in ascending order.

Print one integer — the maximum distance along OxOx axis that the glider can fly from the point where he jumps off the plane to the point where he lands if he can start his flight at any integer coordinate.

3 4
2 5
7 9
10 11

10

5 10
5 7
11 12
16 20
25 26
30 33

18

1 1000000000
1 1000000000

1999999999

In the first example if the glider can jump out at (2,4)(2,4) , then the landing point is (12,0)(12,0) , so the distance is 12−2=10 12−2=10 .

In the second example the glider can fly from (16,10)(16,10) to (34,0)(34,0) , and the distance is 34−16=18 34−16=18 .

In the third example the glider can fly from (−100,1000000000)(−100,1000000000) to (1999999899,0)(1999999899,0) , so the distance is 1999999899−(−100)=19999999991999999899−(−100)=1999999999 .

題意：給你n個無重力地帶，飛機可以從高度h的任意位置開始滑行，問你最遠能滑行多遠。

思路：（orz做的時候想三分，結果wa了，經過網上題解的調教，原來二分就可以了）首先，我們肯定是從某個無重力地帶開始滑行，但是挨個枚舉肯定不行，然後就二分Orz

二分註重的就是個單調性，這題比較隱蔽，我們可以發現從左往右，價值越來越大（無重力地帶的總長度是越來越長，免費長度，相當於白給），另外花費（兩兩無重力地帶之間的區域，即飛機會下降的區域）也是隨著右移越來越大，這樣我們可以預處理價值和花費，註意cost【n】 = 2e9+1,因為最後一個無重力地帶後面是無限長的。

這樣，對於第一個起點，我們擁有高度h可以花費，也就是說找到第一個大於等於高度h的花費，可以用lowerbound；當然，但我們要想後枚舉起點的時候h可以加上該起點之前的前綴和（畢竟終點要在起點之後，二分終點的時候加上起點前的值就相當於從該起點後查詢）

#include<bits/stdc++.h>
using namespace std;

int n,h;
const int maxn = 2e5+5;

int l[maxn];
int r[maxn];

int add[maxn];
int cost[maxn];

int main()
{
    scanf("%d%d",&n,&h);
    for(int i=1;i<=n;i++)
    {
        scanf("%d%d",&l[i],&r[i]);
    }
    cost[n] = 2e9+10;
    for(int i=1;i<n;i++)
    {
        cost[i] = cost[i-1] + l[i+1] - r[i];
        add[i] = add[i-1] + r[i] - l[i];
    }
    add[n] = add[n-1] + r[n] - l[n];
    int ans = 0;
    for(int i=1;i<=n;i++)
    {
        int t = lower_bound(cost+1,cost+1+n,cost[i-1]+h)-cost;
        ans = max(ans,add[t]-add[i-1]+h);
    }
    printf("%d\n",ans);
}

B - Glider Gym - 101911B