一文教你全面掌握用Python實現線性迴歸
全文共4968字,預計學習時長15分鐘或更長

本文旨在為讀者理解和應用線性迴歸時提供參考。雖然線性迴歸演算法很簡單,但是隻有少數人能真正理解其基本原則。
本文首先會深入挖掘線性迴歸理論,理解其內在的工作機制,然後利用Python實現該演算法,為商業問題建模。

理論
線性迴歸或許是學習統計學最簡單的方法。在學習更高階的方法之前,這是一個很好的入門方法。事實上,許多更高階的方法可被視為線性迴歸的延伸。因此,理解好這一簡單模型將為將來更復雜的學習打下良好基礎。
線性迴歸可以很好地回答以下問題:
· 兩個變數間有關係嗎?
· 關係有多強?
· 哪一個變數的影響最大?
· 預測的各個變數影響值能有多精確?
· 預測的目標值能有多精確?
· 其關係是線性的嗎?
· 是否有互動作用?
預估係數
假設僅有一個自變數和因變數,那麼線性迴歸表達如下:
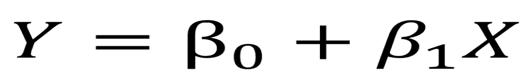
一個自變數和因變數線性模型的方程式
在上圖的方程中,兩個β就是係數。在模型中預測結果需要用到這些係數。
那麼,如何算出這些引數呢?
為此,需要最小化最小二乘法或者誤差平方和。當然,線性模型也不是完美的,也不能準確預測出所有資料,這就意味著實際值和預測值間存在差異。該誤差能用以下方程簡單算出:
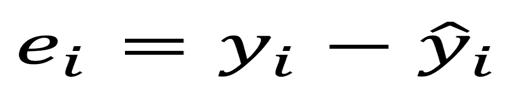
實際值減去預測值
但為什麼要平方誤差呢?
平方誤差,是因為預測值可能大於也可能小於實際值,從而分別產生負或正的誤差。如果沒有平方誤差值,誤差的數值可能會因為正負誤差相消而變小,而並非因為模型擬合好。
此外,平方誤差會加大誤差值,所以最小化平方誤差可以保證模型更好。
下圖有助於更好地理解這個概念:
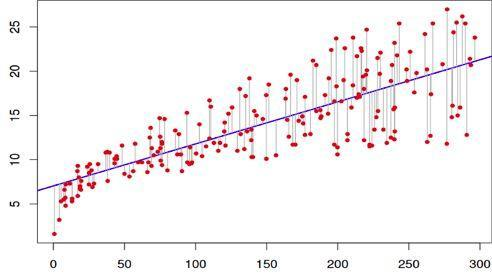
線性擬合數據集
在上述圖表中,紅點是實際值,而藍線是線性模型。灰線展現了預測值和實際值之間的誤差。因此,藍線就是灰線長度平方的最小值。
經過一系列超出本文難度的數學計算,最終可以得到以下這個方程式,用以計算引數。
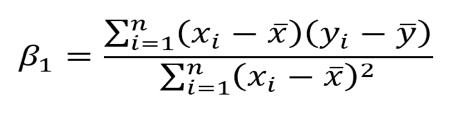
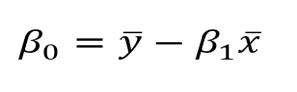
x和y代表平均值
預估係數的相關性
目前已得知係數,那麼如何證明係數與因變數是否相關?
最好的方法就是找到p值。p值被用於量化資料的重要性,它能判斷零假設是否被否定。
什麼是零假設?
所有建模任務都是在自變數和因變數存在一定關聯的假設下進行的。而零假設則正好相反,也就是說自變數和因變數之間沒有任何關聯。
因此,算出每一個係數的p值就能得知,從資料值上來說,該變數對於預估因變數是否重要。一般來說,如果p值小於0.05,那麼自變數和因變數就之間存在強烈關係。
評估模型的準確性
通過找出p值,從資料值上來說,自變數是非常重要的。
如何得知該線性模型是擬合好呢?
通常使用RSE(殘差標準差)和 R 來評估模型。

RSE計算公式
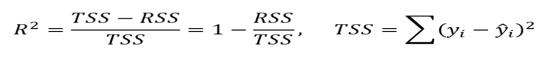
R計算公式
第一個誤差度量很容易理解:殘差越小,模型資料擬合越好(在這種情況下,資料越接近線性關係)。
R可以衡量因變數的變化比例,並用自變數x表述。因此,假設在一個線性方程中,自變數x可以解釋因變數,那麼變化比例就高, R 將接近1。反之,則接近0。

多元線性迴歸理論
在現實生活中,不會出現一個自變數預測因變數的情況。所以,線性迴歸模型是一次只分析一個自變數嗎?當然不是了,實際情況中採取多元線性迴歸。
該方程式和一元線性迴歸方程很像,只不過是再加上預測數和相應的係數。

多元線性迴歸等式。p表示自變數的個數。
評估自變數的相關性
在前文中,通過找出p值來評估一元線性迴歸中自變數的相關性。在多元線性迴歸中,F統計量將被用於評估相關性。
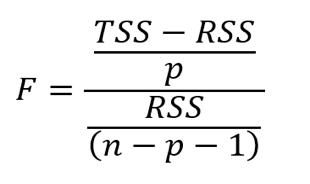
F統計量計算公式。n表示資料量,p表示自變數的個數。
F統計量在整個方程中計算,而p值則針對特定的自變數。如果兩者有強烈的相關性,F大於1。相反,F大約等於1。
比1大多少是足夠大呢?
這是一個很難回答的問題。通常,如果資料中有一個很大的數值的話,F可以僅比1大一點點,而又代表了強烈的相關性。如果資料集中的資料量很小的話,F值一定要比1大很多,才能表示強烈的相關性。
為什麼在這種情況下不能使用p值呢?
因為我們擬合了許多自變數,所以我們需要考慮一個有很多自變數的情況(p值很大)。當自變數的數量較大時,通常會有大約5%的自變數的p值會很小——即使它們在統計上並不顯著。因此,我們使用F統計量來避免將不重要的自變數視為重要的自變數。
評估模型準確性
和一元線性迴歸模型一樣,多元線性迴歸模型的準確性也可以用R來評估。然而,需要注意的是,隨著自變數數量的增加,R的數值也會增大。這是因為模型必然和訓練資料擬合得更好。
但是,這並不意味著該模型在測試資料上(預測未知資料時)也會有很好的表現。
增加干擾
線上性模型中,多元自變數意味著其中一些自變數會對其他自變數產生影響。
比如說,已知一個人年齡和受教育年數,去預測她的薪資。很明顯,年齡越大,受教育時長就越長。那麼,在建模時,要怎樣處理這種干擾呢?
以兩個自變數為例:
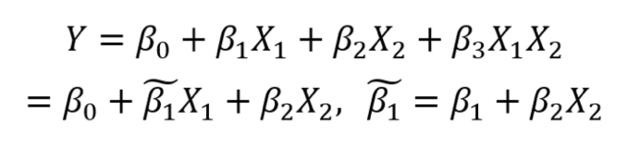
多元線性迴歸中的干擾
從上式可知,我們將兩個自變數相乘,得到一個新的係數。從簡化的公式中可以看到,該係數受到另一個特徵值的影響。
通常來說,在將干擾模型考慮在內時,也需要考慮個體特徵的影響,即使在p值不重要時也要這麼做。這就是分層遞階原則。該原則背後的根據是,如果兩個自變數互相干擾,那麼將它們個體影響考慮在內將會對建模有很小的影響。
以上就是線性迴歸的基本原理。接下來本文將介紹如何在Python中實現一元線性迴歸和多元線性迴歸,以及如何評估兩種模型的模型引數質量和模型整體表現。
強烈建議讀者在閱讀本文之後動手在Jupyter notebook上覆現整個過程,這將有助於讀者充分理解和利用該教程。

那麼開始吧!
本文用到的資料集包括在電視、廣播和報紙上花費的廣告費用及各自帶來的銷售額。
該實驗旨在利用線性代數了解廣告費用對銷售額的影響。
匯入庫
利用Python程式設計有一個好處,就是它可以提供多個庫的渠道,使得我們可以快速讀取資料、繪製資料和執行線性迴歸。
筆者習慣於將所有必要的庫放在程式碼的開頭,使程式碼井然有序。匯入:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
import statsmodels.api as sm
讀取資料
下載資料集後,將資料集放在專案檔案的資料目錄中,讀取資料:
data = pd.read_csv("data/Advertising.csv")
檢視資料時,輸入:
data.head()
得到結果如下:
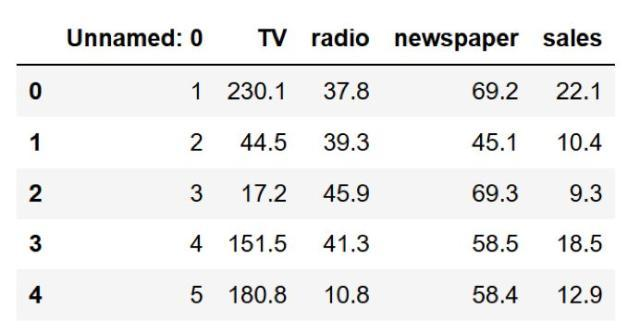
可以看到,“未命名:0”列是多餘的。所以,我們把這一列刪除。
data.drop(['Unnamed: 0'], axis=1)
現在資料已經清理完畢,可以執行線性迴歸了!

簡單線性迴歸
建模
使用簡單線性迴歸建模時,這裡只考慮電視廣告對銷售額的影響。在正式建模之前,首先檢視一下資料。
可以利用matplotlib(一個常用的Python繪製庫)來畫一個散點圖。
plt.figure(figsize=(16, 8))plt.scatter(data['TV'],data['sales'],c='black')plt.xlabel("Money spent on TV ads ($)")plt.ylabel("Sales ($)")plt.show()
執行上述程式碼,可以得到下圖:

電視廣告費用和銷售額散點圖
從圖中可以看到,電視廣告費用和銷售額明顯相關。
基於此資料,可以得出線性近似。操作如下:
X = data['TV'].values.reshape(-1,1)
y = data['sales'].values.reshape(-1,1)
reg = LinearRegression()
reg.fit(X, y)
print("The linear model is: Y = {:.5} + {:.5}X".format(reg.intercept_[0], reg.coef_[0][0]))
就這麼簡單?
對的!對資料集給出一條擬合直線並檢視等式引數就是這麼簡單。在該案例中,可以得到:
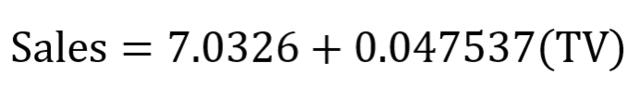
一元線性迴歸等式
接下來將資料擬合線視覺化。
predictions = reg.predict(X)
plt.figure(figsize=(16, 8))plt.scatter(data['TV'],data['sales'],c='black')plt.plot(data['TV'],predictions,c='blue',linewidth=2)plt.xlabel("Money spent on TV ads ($)")plt.ylabel("Sales ($)")plt.show()
可以得到:
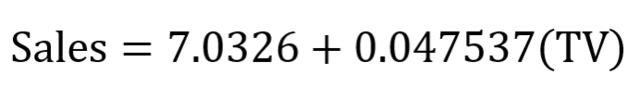
線性擬合
從上圖可以發現,一元線性迴歸模型似乎就可以大致解釋電視廣告費用對銷售額的影響。
評估模型相關性
接下來是檢驗一個模型表現是否良好,需要檢視它的R值和每個係數的p值。
輸入以下程式碼:
X = data['TV']y = data['sales']
X2 = sm.add_constant(X)est = sm.OLS(y, X2)est2 = est.fit()print(est2.summary())
可以得到如下輸出:

R值和p值
觀察兩個係數可以發現,p值雖然並不一定是0,但是非常低。這意味著這些係數和目標值(此處即銷售額)之間有很強烈的聯絡。
同時可以觀察到,R值為0.612。這說明大約60%的銷售額變化是可以由電視廣告花費來解釋的。這樣的結果是合理的。但是,這一定不是可以用來準確預測銷售額的最好的結果。在報紙和廣播廣告上的花費必定對銷售額有一定的影響。
接下來將檢測多元線性迴歸模型是否能取得更好的結果。

多元線性迴歸
建模
和一元線性迴歸的建模過程一樣,定義特徵值和目標變數,並利用scikit-learn庫來執行線性迴歸模型。
Xs = data.drop(['sales', 'Unnamed: 0'], axis=1)
y = data['sales'].reshape(-1,1)
reg = LinearRegression()
reg.fit(Xs, y)
print("The linear model is: Y = {:.5} + {:.5}*TV + {:.5}*radio + {:.5}*newspaper".format(reg.intercept_[0], reg.coef_[0][0], reg.coef_[0][1], reg.coef_[0][2]))
就是這麼簡單!根據上述程式碼可以得到如下等式:
多元線性迴歸等式
當然,由於一共有四個變數,這裡無法把三種廣告媒介對銷售額的影響視覺化,那將需要一個四維圖形。
需要注意的是,報紙的係數是負數,並且很小。這和模型有關嗎?為了回答這個問題,我們需要計算模型的F統計量、R值以及每個係數的p值。
評估模型相關性
正如你所想,這一步驟和一元線性迴歸模型中的相應步驟非常相似。
X = np.column_stack((data['TV'], data['radio'], data['newspaper']))
y = data['sales']
X2 = sm.add_constant(X)
est = sm.OLS(y, X2)
est2 = est.fit()
print(est2.summary())
可以得到:
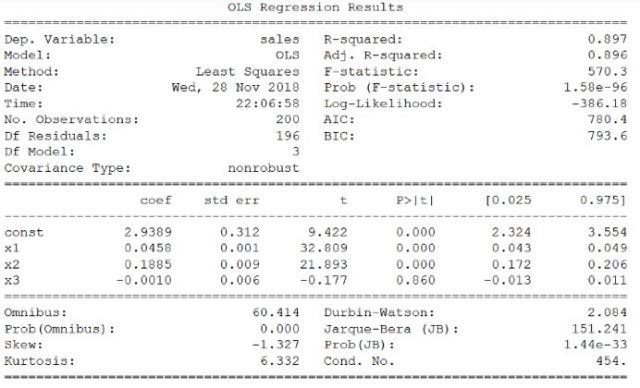
R值,p值和F統計量
可以看到,多元線性迴歸模型的R值比一元線性迴歸模型要高得多,達到了0.897!
其F統計量為570.3。這比1要大得多。由於本文使用的資料集比較小(只有200個數據),這說明廣告花費和銷售額之間有強烈的聯絡。
最後,由於本文只用了三個自變數可以利用p值來衡量它們是否與模型相關。從上表可以發現,第三個係數(即報紙廣告的係數)的p值比另外兩個要大。這說明從資料來看,報紙廣告花費並不重要。去除這個自變數可能會使R有輕微下降,但是可以幫助得到更加準確的預測結果。
線性迴歸模型也許不是表現最好的模型,但瞭解線性迴歸是非常重要的,這將幫助我們打好基礎,理解更加複雜的統計學方法。
留言 點贊 關注
我們一起分享AI學習與發展的乾貨
歡迎關注全平臺AI垂類自媒體 “讀芯術”
(新增小編微信:dxsxbb,加入讀者圈,一起討論最新鮮的人工智慧科技哦
