08 決策樹與隨機森林
阿新 • • 發佈:2019-11-26
08 決策樹與隨機森林
決策樹之資訊理論基礎
認識決策樹
來源: 決策樹的思想來源非常樸素,程式設計中的條件分支結構就是if - then 結構,最早的決策樹就是利用這類結構分割資料的一種分類學習方法。
舉例:是否見相親物件
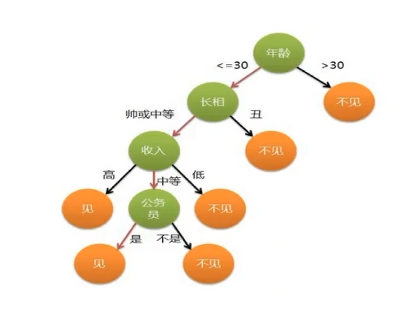
資訊的度量和作用
- 克勞德 .艾爾伍德 .夏農:資訊理論創始人,密西根大學學士,麻省理工學院博士。 1948年發表了劃時代論文 - 通訊的數學原理,奠定了現代資訊理論的基礎。
資訊的單位: 位元 (bit)

- 舉例: 以32支球隊爭奪世界盃冠軍
如果不知道任何球隊的資訊,每支球隊得冠概率相等。
以二分法預測,最少需要使用5次才能預測到準確結果。 5 = log32 (以2為底)
5 = -(1/32log1/32 + 1/32log1/32 + ......)開放一些資訊,則小於5bit, 如1/6 德國,1/6 巴西, 1/10 中國
5 > -(1/6log1/4 + 1/6log1/4 + ....)
- 資訊熵:
- “誰是世界盃冠軍”的資訊量應該比5 bit少, 它的準確資訊量應該是:
- H = -(p1logp1 + p2logp2 + p3logp3 +......p32logp32 ) Pi 為第i支球隊獲勝的概率
- H 的專業術語就是資訊熵,單位為位元
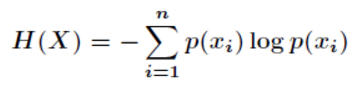
決策樹的劃分以及案例
資訊增益
定義: 特徵A對訓練資料集D的資訊增益g(D,A), 定義為集合D的資訊熵H(D)與特徵A給定條件下D的資訊條件熵H(D|A) 之差,即:
g(D,A) = H(D) - H(D | A)
注: 資訊增益表示得知特徵 X 的資訊而使得類 Y的資訊的不確定性減少的程度。

以不同特徵下的信貸成功率為例
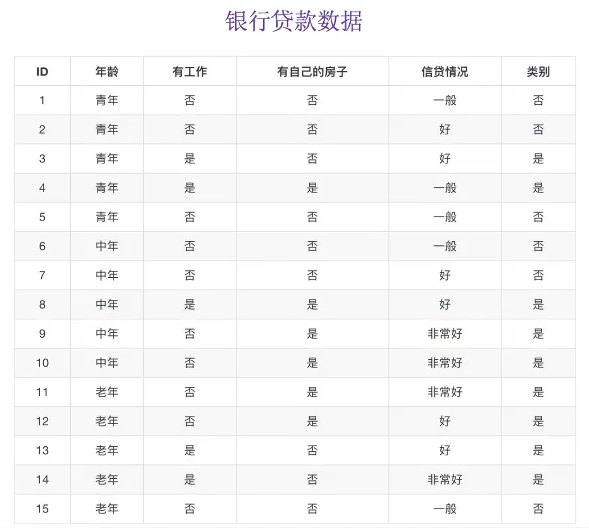
- H(D) = -(9/15log(9/15) + 6/15log(6/15)) = 0.971 # 以類別進行判斷,只有是否兩種類別
- gD,年紀) = H(D) - H(D'|年紀) = 0.971 - [1/3H(青年)+ 1/3H(中年)+ 1/3H(老年)] # 三種年紀對應的目標值均佔1/3
- H(青年) = -(2/5log(2/5) + 3/5log(3/5)) # 青年型別中,類別的目標值特徵為(2/5, 3/5)
- H(中年) = -(2/5log(2/5) + 3/5log(3/5))
- H(老年) = -(4/5log(2/5) + 1/5log(3/5))
令A1, A2, A3, A4 分別表示年齡,有工作,有房子和信貸情況4個特徵,則對應的資訊增益為:
g(D,A1) = H(D) - H(D|A1)
其中,g(D,A2) = 0.324 , g(D,A3) = 0.420 , g(D,A4) = 0.363
相比而言,A3特徵(有房子)的資訊增益最大,為最有用特徵。
所以決策樹的實際劃分為:
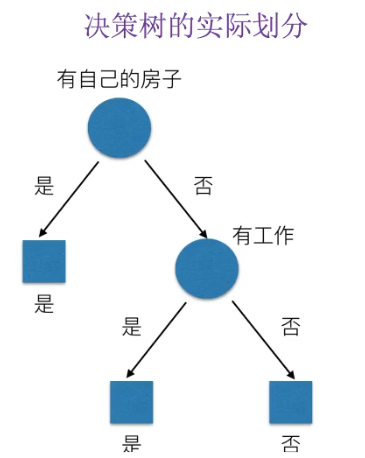
常見決策樹使用的演算法
- ID3
- 資訊增益,最大原則
- C4.5
- 資訊增益比最大原則 (資訊增益佔原始資訊量的比值)
- CART
- 迴歸樹: 平方誤差最小
- 分類樹: 基尼係數最小原則 (劃分的細緻),sklearn預設的劃分原則
Sklearn決策樹API
- sklearn.tree.DecisionTreeClassifier(criterion='gini', max_depth=None, random_state=None)
- criterion (標準): 預設基尼係數,也可以選用資訊增益的熵‘entropy’
- max_depth: 樹的深度大小
- random_state: 隨機數種子
- 決策樹結構
sklearn.tree.export_graphviz() 匯出DOT檔案格式
- estimator: 估算器
- out_file = "tree.dot" 匯出路徑
- feature_name = [,] 決策樹特徵名
決策樹預測泰坦尼克號案例
import pandas as pd
from sklearn.feature_extraction import DictVectorizer
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier, export_graphviz
"""
泰坦尼克資料描述事故後乘客的生存狀態,該資料集包括了很多自建旅客名單,提取的資料集中的特徵包括:
票的類別,存貨,等級,年齡,登入,目的地,房間,票,船,性別。
乘坐等級(1,2,3)是社會經濟階層的代表,其中age資料存在缺失。
"""
def decision():
"""
決策樹對泰坦尼克號進行預測生死
:return: None
"""
# 1.獲取資料
titan = pd.read_csv('./titanic_train.csv')
# 2.處理資料,找出特徵值和目標值
x = titan[['Pclass', 'Age', 'Sex']]
y = titan[['Survived']]
# print(x)
# 缺失值處理 (使用平均值填充)
x['Age'].fillna(x['Age'].mean(), inplace=True)
print(x)
# 3.分割資料集到訓練集和測試集
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.25)
# 4. 進行處理(特徵工程) 特徵,類別 --> one_hot編碼
dict = DictVectorizer(sparse=False)
x_train = dict.fit_transform(x_train.to_dict(orient='records'))
print(dict.get_feature_names())
x_test = dict.transform(x_test.to_dict(orient='records')) # 預設一行一行轉換成字典
print(x_train)
# 5. 用決策樹進行預測
dec = DecisionTreeClassifier()
dec.fit(x_train, y_train)
# 預測準確率
print("預測的準確率:", dec.score(x_test, y_test))
# 匯出決策樹
export_graphviz(dec, out_file='./tree.dot', feature_names=['Pclass', 'Age', 'Sex'])
return None
if __name__ == '__main__':
decision()
