之前我們介紹過BERT+CRF來進行命名實體識別，並對其中的BERT和CRF的概念和作用做了相關的介紹，然對於CRF中的最優的標籤序列的計算原理，我們只提到了維特比演算法，並沒有做進一步的解釋，本文將對維特比演算法做一個通俗的講解，以便大家更好的理解CRF為什麼能夠得到最優的標籤序列。

通過閱讀本文你將能回答如下問題：

• 什麼是維特比演算法？
• 為什麼說維特比演算法是一種動態規劃演算法？
• 維特比演算法具體怎麼實現？

首先，讓我們簡單回顧一下BERT和CRF在命名實體識別中各自的作用：
命名實體識別中，BERT負責學習輸入句子中每個字和符號到對應的實體標籤的規律，而CRF負責學習相鄰實體標籤之間的轉移規則。詳情可以參考這篇文章CRF在命名實體識別中是如何起作用的？。該文章中我們對CRF做了簡單易懂的介紹，其中提到CRF的損失函式計算要用到最優路徑，因為CRF的損失函式是求最優路徑的概率佔所有路徑概率和的比例，而我們的目標是最大化這個比例。那麼這裡就涉及到計算最優路徑的問題。這裡的路徑在命名實體識別的例子中，就是最終輸出的與句子中的字或符號一 一對應的標籤序列。不同標籤序列的順序組成了不同的路徑。而CRF就是要找出最正確的那條標籤序列路徑，也就是說這條標籤路徑的概率將是所有路徑中最大的，那麼我們可以窮舉出所有可能的標籤路徑，計算出每條路徑的概率和，然後比較出最大的那條，但是這樣做的代價太大了，所以crf選擇了一種稱為維特比的演算法來求解此類問題。

維特比演算法（英語：Viterbi algorithm）是一種動態規劃演算法。它用於尋找最有可能產生觀測事件序列的維特比路徑。

看看下面這個命名實體識別的例子：

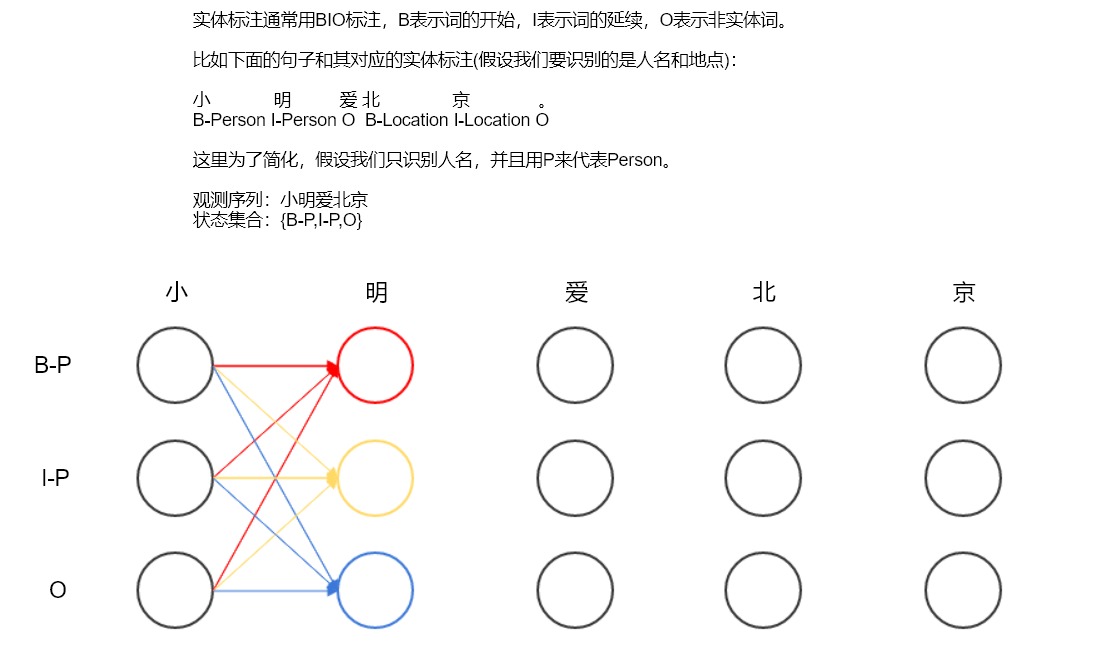
上圖共有5層(觀測序列的長度)，每層3個節點(狀態的個數)，我們的目標就是找到從第一層到第五層的最優路徑。
首先，我們分別計算紅、黃、藍三個節點的輸入連線的概率，以紅色節點舉例，我們先假設紅色節點在最優路徑上，那麼輸入到該節點的三條連線中，概率最大的那條一定在最優路徑上，同理，我們再分別假設黃色和藍色節點在最優路徑上，我們也能各找到一條概率最大的連線，這樣就得到了下面的圖：

然後，我們接著剛才的思路繼續找後面一層的三條最優的連線：

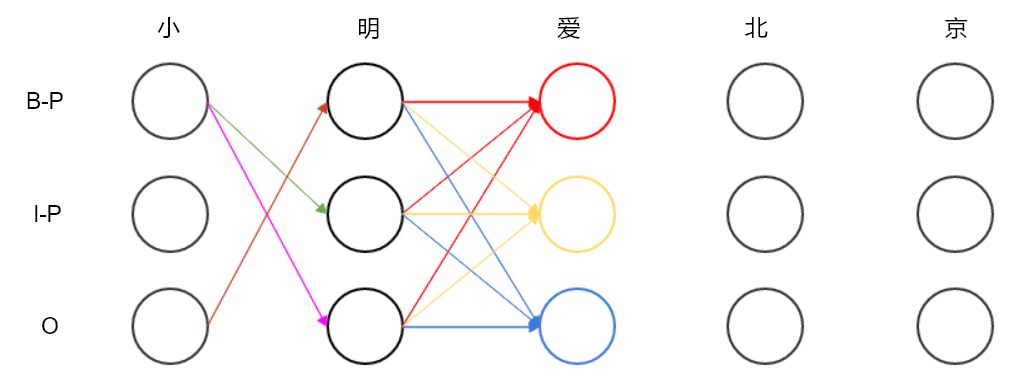
假設找到的最優連線如下：

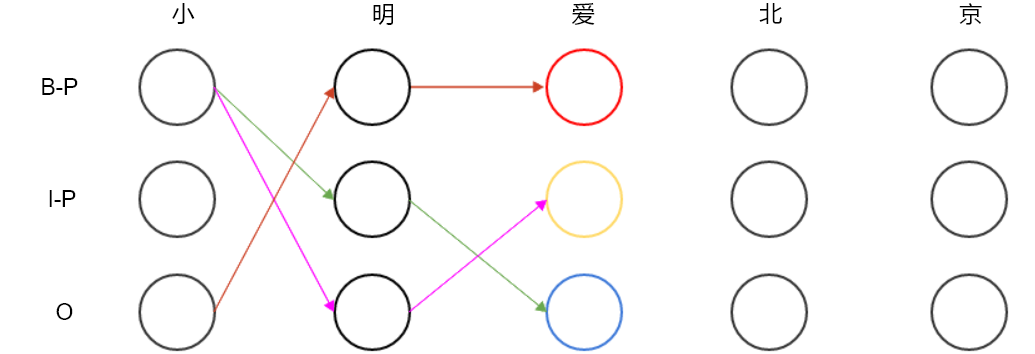
然後，接著在後面的層應用這個方法：

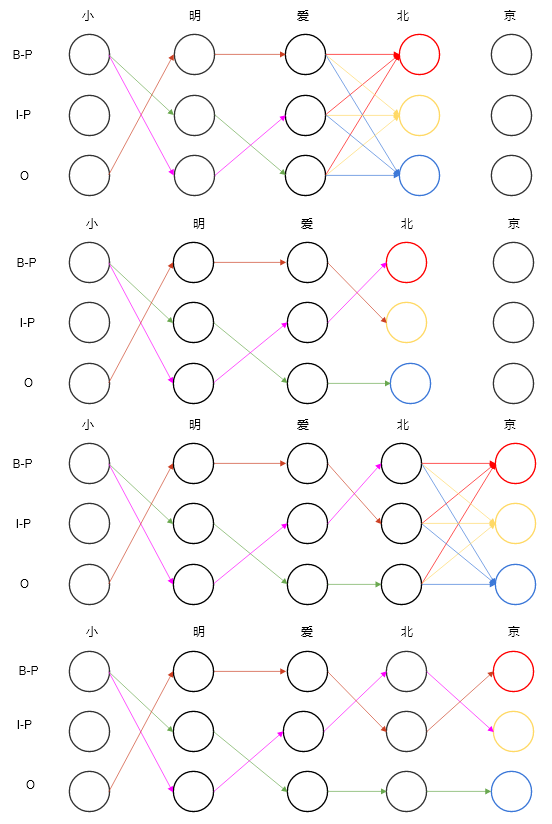
此時，看上面最後一張圖，我們有了3條候選最優路徑，分別是棕色、綠色和紫色，用標籤來表達如下：

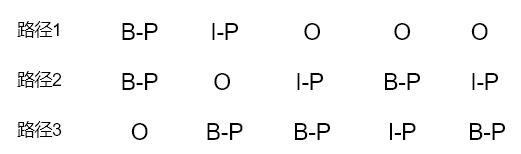
那麼哪條才是最優路徑呢？
就是看哪條路徑的概率和最大，那條路徑就是最優路徑。
但是在實際實現的時候，一般會在計算各層的最優候選連線的時候，就記錄下前繼連線的概率和，並記錄下對應的狀態節點索引(這裡將已經計算出的結果記錄下來供後續使用的方式，就是維特比演算法被稱為動態規劃演算法的原因)，這樣到最後一層的時候，最後一層各候選連線中概率最大的，就是在最優路徑上的那條連線了，然後從這條連線回溯，找出完整的路徑就是最優路徑了。

一直在說概率最大的路徑，那麼這個概率具體指什麼呢？
還記得上一篇文章介紹條件隨機場(CRF)的時候提到，條件隨機場其實是給定了觀測序列的馬爾可夫隨機場，在一階馬爾可夫模型中，定義了以下三個概念：

• 狀態集合Q，對應到上面的例子就是：
  {B-P, I-P, O}
• 初始狀態概率向量Π，對應到上面的例子就是：
  {B-P:0.3, I-P:0.2, O:0.5}
  這裡的概率數值是隨便假設的，僅為了方便舉例說明。
• 狀態轉移概率矩陣A：
  

CRF中給定了觀測序列做為先驗條件，對應到上面的例子就是：

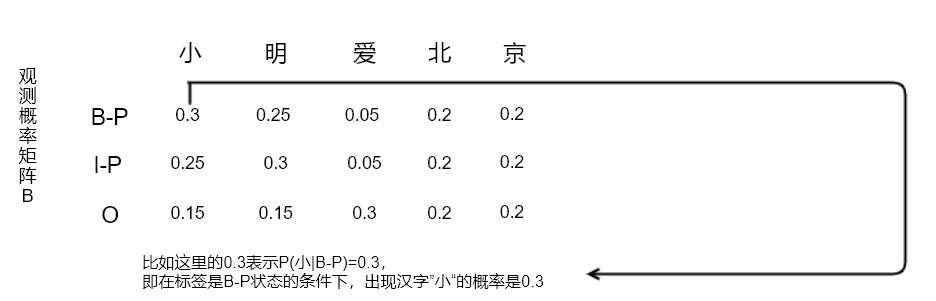
其中的概率數值同樣是隨便假設的，為了方便舉例。

下圖中紅色節點的概率(可以看成是一個虛擬的開始節點到該節點的連線的概率)的計算方式如下：
初始狀態為B-P的概率Π(B-P) * 該節點的觀測概率P(小|B-P)

下圖中紅色節點的三條連線概率的計算方式如下：
上一層對應節點的概率 * 上層對應節點到該節點的轉移概率 * 該節點的觀測概率P(明|B-P)

其它層之間的節點連線的概率同理計算可得，然後通過上面介紹的維特比演算法過程就可以計算出最優路徑了。

ok,本篇就這麼多內容啦~，感謝閱讀O(∩_∩)O。

相關推薦