迴歸損失函式2 : HUber loss,Log Cosh Loss,以及 Quantile Loss
均方誤差(Mean Square Error,MSE)和平均絕對誤差(Mean Absolute Error,MAE) 是迴歸中最常用的兩個損失函式,但是其各有優缺點。為了避免MAE和MSE各自的優缺點,在Faster R-CNN和SSD中使用\(\text{Smooth} L_1\)損失函式,當誤差在\([-1,1]\) 之間時,\(\text{Smooth} L_1\)損失函式近似於MSE,能夠快速的收斂;在其他的區間則近似於MAE,其導數為\(\pm1\),不會對離群值敏感。
本文再介紹幾種迴歸常用的損失函式
- Huber Loss
- Log-Cosh Loss
- Quantile Loss
Huber Loss
Huber損失函式(\(\text{Smooth} L_1\)損失函式是其的一個特例)整合了MAE和MSE各自的優點,並避免其缺點
\[
L_\delta(y,f(x)) = \left \{ \begin{array}{c} \frac{1}{2} (y - f(x))^2 & \mid y - f(x) \mid \leq \delta \\ \delta \mid y-f(x) \mid - \frac{1}{2} \delta ^2 & \text{otherwise}\end{array}\right.
\]
\(\delta\) 是Huber的一個超引數,當真實值和預測值的差值\(\mid y- f(x) \mid \leq \delta\) 時,Huber就是MSE;當差值在\((-\infty,\delta )\)或者 \((\delta,+\infty)\) 時,Huber就是MAE。這樣,當誤差較大時,使用MAE對離群點不那麼敏感;在誤差較小時使用MSE,能夠快速的收斂;
這裡超引數\(\delta\)的值的設定就較為重要,和真實值的差值超過該值的樣本為異常值。誤差的絕對值小於\(\delta\) 時,使用MSE;當誤差大於\(\delta\) 時,使用MAE。
下圖給出了不同的\(\delta\) 值,Huber的函式曲線。
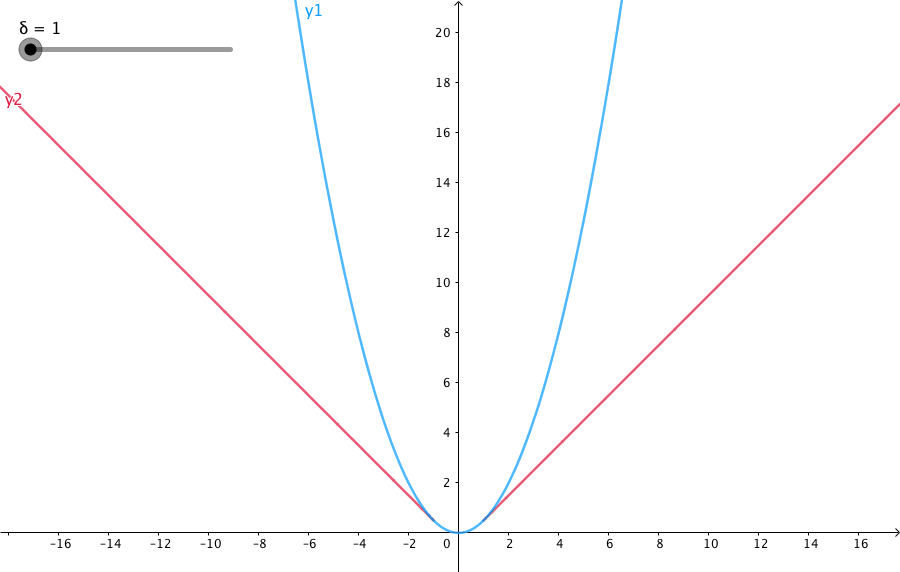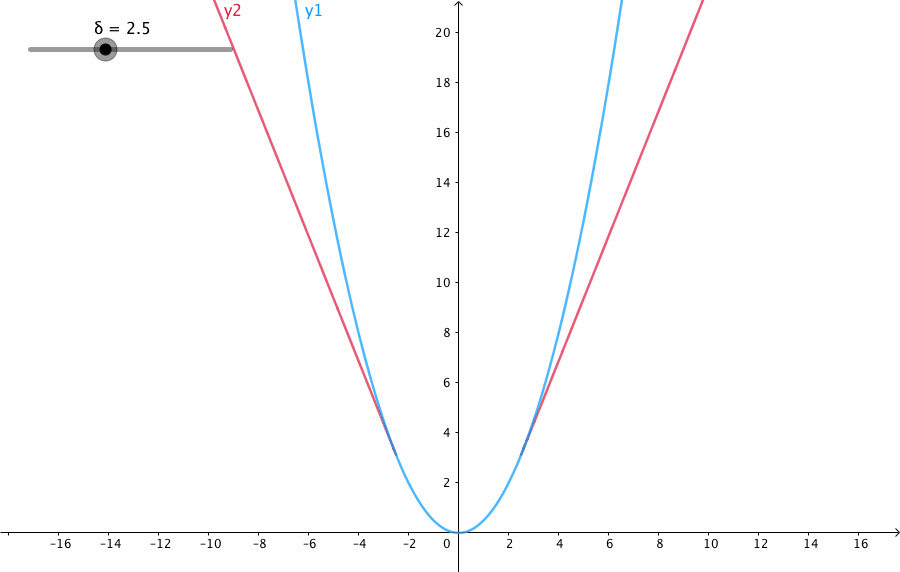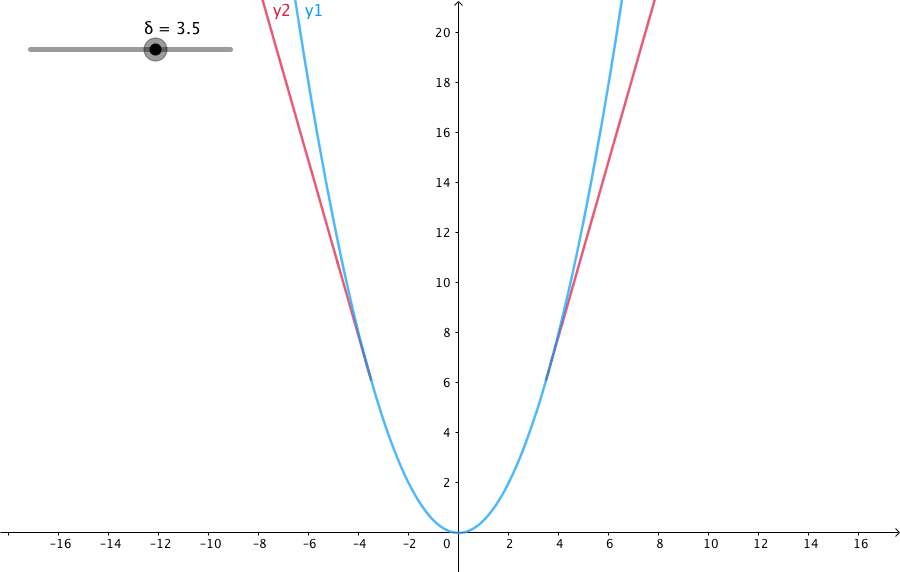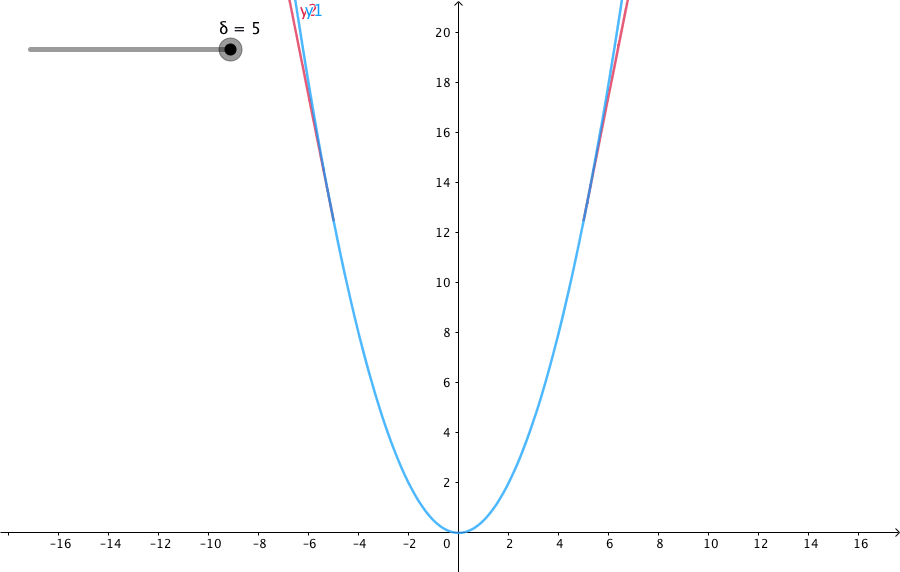
橫軸表示真實值和預測值的差值,縱軸為Huber的函式值。可以看出,\(\delta\) 越小其曲線越趨近於MSE;越大,越趨近於MAE。
另外,使用MAE訓練神經網路最大的一個問題就是不變的大梯度,這可能導致在使用梯度下降快要結束時,錯過了最小點。而對於MSE,梯度會隨著損失的減小而減小,使結果更加精確。
在這種情況下,Huber損失就非常有用。它會由於梯度的減小而落在最小值附近。比起MSE,它對異常點更加魯棒。因此,Huber損失結合了MSE和MAE的優點。但是,Huber損失的問題是我們可能需要不斷調整超引數\(\delta\) 。
\(\text{Smooth }L_1\) 損失函式可以看作超引數\(\delta = 1\) 的Huber函式。
Log-Cosh Loss
Log-Cosh是比\(L_2\) 更光滑的損失函式,是誤差值的雙曲餘弦的對數
\[
L(y,f(x)) = \sum_{i=1}^n\log \cosh(y-f(x))
\]
其中,\(y\)為真實值,\(f(x)\) 為預測值。
對於較小的誤差$\mid y - f(x) \mid $ ,其近似於MSE,收斂下降較快;對於較大的誤差\(\mid y - f(x) \mid\) 其近似等於\(\mid y-f(x) \mid - log(2)\) ,類似於MAE,不會受到離群點的影響。 Log-Cosh具有Huber 損失的所有有點,且不需要設定超引數。
相比於Huber,Log-Cosh求導比較複雜,計算量較大,在深度學習中使用不多。不過,Log-Cosh處處二階可微,這在一些機器學習模型中,還是很有用的。例如XGBoost,就是採用牛頓法來尋找最優點。而牛頓法就需要求解二階導數(Hessian)。因此對於諸如XGBoost這類機器學習框架,損失函式的二階可微是很有必要的。但Log-cosh損失也並非完美,其仍存在某些問題。比如誤差很大的話,一階梯度和Hessian會變成定值,這就導致XGBoost出現缺少分裂點的情況。
Quantile Loss 分位數損失
通常的迴歸演算法是擬合訓練資料的期望或者中位數,而使用分位數損失函式可以通過給定不同的分位點,擬合訓練資料的不同分位數。 如下圖
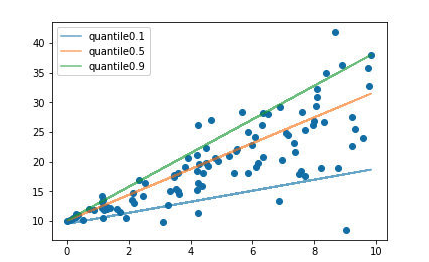
設定不同的分位數可以擬合出不同的直線。
分位數損失函式如下:
\[
L_{quantile} = \frac{1}{N}\sum_{i=1}^N \amalg_{y > f(x)}(1-\gamma)\mid y-f(x)\mid + \amalg_{y < f(x)}\gamma \mid y - f(x) \mid
\]
該函式是一個分段函式,\(\gamma\) 為分位數係數,\(y\)為真實值,\(f(x)\)為預測值。根據預測值和真實值的大小,分兩種情況來開考慮。\(y > f(x)\) 為高估,預測值比真實值大;\(y < f(x)\)為低估,預測值比真實值小,使用不同過得係數來控制高估和低估在整個損失值的權重 。
特別的,當\(\gamma = 0.5\) 時,分位數損失退化為平均絕對誤差MAE,也可以將MAE看成是分位數損失的一個特例 - 中位數損失。下圖是取不同的中位點\([0.25,0.5,0.7]\) 得到不同的分位數損失函式的曲線,也可以看出0.5時就是MAE。
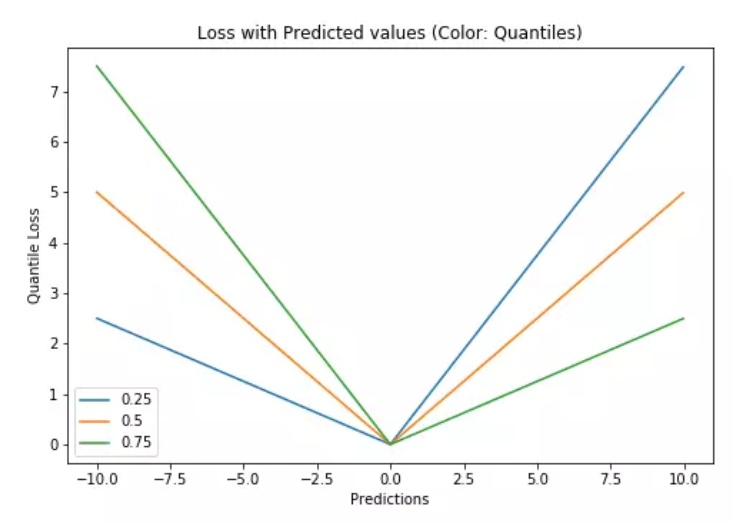
總結
均方誤差(Mean Square Error,MSE)和平均絕對誤差(Mean Absolute Error,MAE) 可以說是迴歸損失函式的基礎。但是MSE對對離群點(異常值)較敏感,MAE在梯度下降的過程中收斂較慢,就出現各種樣的分段損失函式,在loss值較小的區間使用MSE,loss值較大的區間使用MAE。
- Huber Loss ,需要一個超引數\(\delta\) ,來定義離群值。$ \text{smooth } L_1$ 是\(\delta = 1\) 的一種情況。
- Log-Cosh Loss, Log-Cosh是比\(L_2\) 更光滑的損失函式,是誤差值的雙曲餘弦的對數.
- Quantile Loss , 分位數損失,則可以設定不同的分位點,控制高估和低估在loss中佔的比重。
