資料探勘篇——特徵工程之特徵降維
阿新 • • 發佈:2020-03-16
在業界廣泛流傳著一句話:資料和特徵決定了機器學習的上限,而模型和演算法只是逼近這個上限而已。
由此可見,資料和特徵是多麼的重要,而在資料大多數場景下,資料已經就緒,不同人對於同樣的資料處理得到的特徵卻千差萬別,最終得到的建模效果也是高低立現。從資料到特徵這就要從特徵工程說起了...
0. 特徵工程
首先介紹下,特徵工程是什麼:利用資料領域的相關知識來建立能夠使機器學習演算法達到最佳效能的特徵的過程[1.wiki]。特徵工程是一個較大領域,它通常包括特徵構建、特徵提取和特徵選擇這三個子模組,重要性排序:特徵構建>特徵提取>特徵選擇。- 特徵構建:從原始資料中構建出特徵,有時也稱作特徵預處理,包括缺失值處理、異常值處理、無量綱化(標準化/歸一化)、啞編碼等。
- 特徵提取:將原特徵轉換為一組具有明顯物理意義或統計意義或核的新特徵。
- 特徵選擇:從特徵集合中挑選一組最具統計意義的特徵子集。
1. 特徵降維
WHAT:將高維空間的特徵通過刪減或變換轉為低維空間特徵 WHY:降低時間/空間複雜度、降低提取特徵開銷、降噪、提升魯棒性、增強可解釋性、便於視覺化; HOW:主要有兩種方式,即特徵選擇和特徵提取。1.1 特徵選擇(子集篩選):
特徵選擇方法主要分為三種:
- Filter:過濾式;按權重排序,不涉及到學習器,排序規則一般有方差法、相關係數法、互資訊法、卡方檢驗法、缺失值比例法(注意受範圍影響的方法需先歸一化)[2.zhihu]。
- 方差法:計算各個特徵的方差,然後根據閾值,選擇方差大於閾值的特徵。可使用sklearn.feature_selection庫的VarianceThreshold類來實現。
- 缺失值比例法:計算各個特徵的缺失值比例,將缺失值比例較大的特徵過濾掉。
- 相關係數法:計算特徵與輸出值的相關係數以及相關係數的 P值(常見的有:皮爾森相關係數用於數值特徵的線性檢驗,秩相關係數用於類別特徵的單調性檢驗)。
- 互資訊法:計算定性特徵與輸出值的相關性(運用了資訊熵理論),決策樹學習中的資訊增益等價於訓練資料集中類與特徵的互資訊。
-
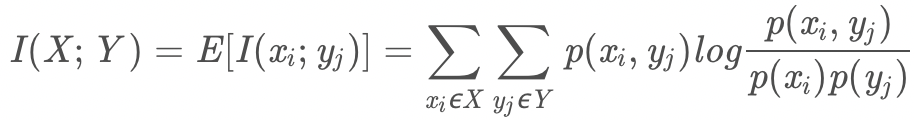
- 卡方檢驗法:對於每個特徵與輸出值,先假設獨立,再觀察實際值與理論值的偏差來確定假設的正確性,即是否相關。
- Embedded:嵌入式;確定模型過程中自動完成重要特徵挑選,基於懲罰項如嶺迴歸(L2正則)、LASSO(L1正則),基於樹模型如GBDT、決策樹[3.cnblog]。
- Wrapper:封裝式;用學習器的效能評判不同特徵子集的效果,特徵子集生成方式:完全搜尋(前向&後向)、啟發式搜尋、隨機搜尋[3.cnblog]。
1.2 特徵提取(投影or轉換):
- 線性方法[4.csdn]:
- PCA:主成分分析;理論:通過正交變換將原始的 n 維資料集變換到一個新的被稱做主成分的資料集中,變換後的結果中第一個主成分具有最大的方差值;
- 特點:無監督,儘量少維度保留儘量多原始資訊(均方誤差最小),期望投影維度上方差最大,不考慮類別,去相關性,零均值化,喪失可解釋性
- ICA:獨立成分分析;將原特徵轉化為相互獨立的分量的線性組合;PCA一般作為ICA的預處理步驟[5.zhihu]。
- LDA:線性判別分析,有監督,儘可能容易被區分(高內聚、低耦合)[6.cnblog]。
- SVD:奇異值分解,可用於PCA、推薦、潛在語義索引LSI,可並行,可解釋性不強
- 非線性方法:
- LLE:區域性線性嵌入,非線性降維(基於圖),保持原有流行結構
- LE:拉普拉斯特徵對映,非線性(基於圖),相互有聯絡的點儘可能靠近
- t-SNE:t分佈隨機臨近嵌入,將歐幾里得距離轉為條件概率表達點與點之間的相似度[7.datakit]。
- AE:自動編碼器
- 聚類
特徵降維方法對比先介紹到這裡,更多內容後續繼續分解~
轉載請註明出處:資料探勘篇——特徵工程之特徵降維(https://www.cnblogs.com/webary/p/12498886.html)
參考連結:
1.wiki:https://en.wikipedia.org/wiki/Feature_engineering
2.zhihu:https://www.zhihu.com/question/28641663
3.cnblog:https://www.cnblogs.com/pinard/p/9032759.html
4.csdn:https://blog.csdn.net/yujianmin1990/article/details/48223001
5.zhihu:https://www.zhihu.com/search?type=content&q=PCA%20ICA
6.cnblog:https://www.cnblogs.com/LeftNotEasy/archive/2011/01/08/lda-and-pca-machine-learning.html
7.datakit:http://www.datakit.cn/blog/2017/02/05/t_sne_full.
