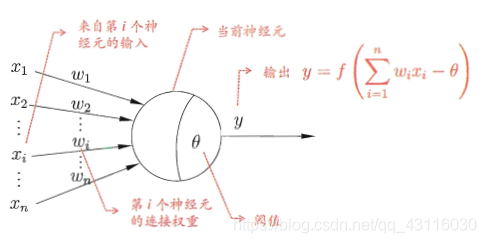
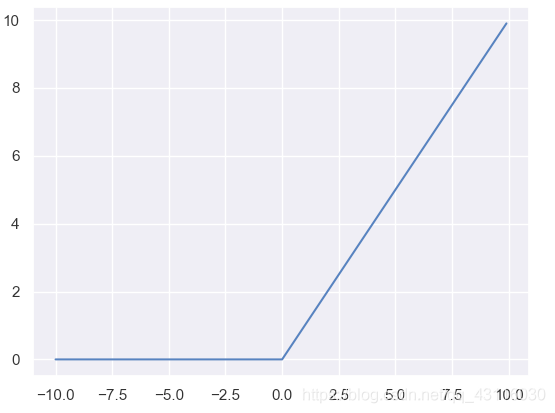
[toc] #### 一、神經元模型 ##### 1.1 M-P神經元   **神經元**（***neuron***）模型是神經網路的基本組成部分，它參考了生物神經元的工作原理：通過多個樹突接收輸入，在神經元進行處理後，如果電平訊號超過某個**闕值**（***threshold***），那麼該神經元就會被啟用並通過一個軸突向其他神經元傳送訊號。對上述流程進行數學抽象，便可以得到如下的**M-P神經元模型**：   神經元模型將接收到的總輸入和與神經元的闕值進行比較，然後通過**激勵函式**（***activation function***）處理以產生神經元的輸出。 ##### 1.2 激勵函式   常見的激勵函式通常有以下幾種： ###### 1.2.1 單位階躍函式 $$ f(z)=\begin{cases} 1,\qquad z>=0\\0,\qquad z<0\end{cases} $$ ###### 1.2.2 logistic函式（sigmoid） $$ f(z)=\frac{1}{1+e^{-z}} \qquad f'(z)=f(z)(1-f(z)) $$ ###### 1.2.3 tanh函式（雙曲正切函式） $$ f(z)=\frac{e^z-e^{-z}}{e^z+e^{-z}} \qquad f'(z)=1-f(z)^2 $$

###### 1.2.4 ReLU（修正線性單元） $$ f(z)=\frac{|z|+z}{2} \qquad f'(z)=\begin{cases}1,\qquad z>=0\\0,\qquad z<0 \end{cases} $$ ###### 1.2.5 激勵函式對比 激勵函式|相對優勢|相對劣勢 -|-|- 階躍函式|當輸入大於闕值返回1，小於闕值返回0，符合理想狀態的神經元模型|曲線不光滑，不連續 Sigmoid|曲線光滑；能夠用於表示正例的概率|可能造成梯度消失；中心點為0.5 Tanh|曲線光滑；中心點為0；收斂較logistic快|可能造成梯度消失 ReLU|不會造成梯度消失；收斂更快|當訓練迭代一定次數後可能導致權重無法繼續更新 ##### 1.3 羅森布拉特感知器   **羅森布拉特感知器**（***Perceptron***）是最早最基礎的神經元模型，它所採用的激勵函式是單位階躍函式。由於階躍函式曲線不連續光滑，且可導區域導數為0，所以其有一套獨特的學習規則： $$ w_{new}=w_{old}+\Delta w\qquad \Delta w=\eta(y-y^*)x $$   如何理解這個學習規則？看下面的例子： 1）分類正確： $$ \Delta w=\eta(0-0)x=0\qquad\Delta w=\eta(1-1)x=0 $$   不再進行更新。 2）分類錯誤： $$ \Delta w=\eta(1-0)x=\eta x\qquad\Delta w=\eta(0-1)x=-\eta x $$   可見，在類標分類錯誤的情況下，感知器會讓權值向正確的標記方向移動。 ##### 1.4 Adaline（自適應線性神經元）   **自適應線性神經元**是普通的感知器的改進。Adaline以線性函式$h(x)=x$為激勵函式，提出了**代價函式**的概念，並且使用了**梯度下降法**來最小化代價函式。其採用均方誤差來作為代價函式： $$ J(x_i,w)=\frac{1}{2m}\sum^{m}_{i=1}{(y_i-h(x_i))^2} $$   那麼對引數$w$的求解則等價於求解：$w=\arg\min_wJ(x_i,w)$。使$J$對$w$求偏導，易得： $$ \frac{\partial J}{\partial w}=\frac{1}{m}\sum^{m}_{i=1}{(y_i-h(x_i))h'(x_i)}=\frac{1}{m}\sum^{m}_{i=1}{(h(x_i)-y_i)x_i} $$ 那麼則有： $$ \Delta w=-\eta\frac{\partial J}{\partial w}=\frac{\eta}{m}\sum^{m}_{i=1}(y_i-h(x_i))x_i\qquad w^*=w+\Delta w $$ #### 二、神經網路模型 ##### 2.1 線性不可分問題   考慮以下問題：**如何讓計算機學得**異或**的計算能力？**   通過繪製決策邊界不難發現，對於以下資料集： $$ X=<(0,0),(0,1),(1,0),(1,1)>\qquad y=<0,1,1,0> $$ 無法通過一個線性超平面畫出該資料集的決策邊界：

  即，異或問題是一個**線性不可分**問題。   單個神經元模型只能通過劃分線性超平面來進行分類，那麼想要解決非線性可分問題，則可以考慮使用效能更強大的多層神經網路。 ##### 2.2 多層前饋神經網路   將多個神經元模型按照一定的次序進行組合便可以生成一個性能強大的**神經網路**（***neural network***，**NN**）。神經網路模型有很多種類，這裡介紹最常見的**多層前饋神經網路**。   上圖是一個具有一個輸入層、一個隱藏層和一個輸出層的三層前饋型神經網路。每一層分別有$d,q,l$個神經元，其中，只有隱藏層和輸出層的神經元是功能神經元（包含激勵函式）。假設神經網路的輸入為$x=(x_1,...,x_i,...,x_d)$，輸入層神經元$i$到隱藏層神經元$h$的權重表示為$w^0_{ih}$，隱藏層神經元$h$到輸出層神經元$j$的權重表示為$w^1_{hj}$。那麼便可以求得： 1）第$h$個隱藏層神經元的輸入和輸出為： $$ \alpha_h=\sum^{d}_{i=1}{w^0_{ih}x_i}\qquad b_h=h(\alpha_h) $$ 2）第$l$個輸出層神經元的輸入和輸出為： $$ \beta_j=\sum^{q}_{h=1}{w^1_{hj}b_h}\qquad y_j=h(\beta_j) $$   以上便是多層前饋神經網路模型的**前向傳播**（***forward propagation***）過程。而前向傳播需要的權值引數，則需要通過學習得到。 #### 三、神經網路學習：誤差逆傳播   神經網路的學習過程比神經元模型複雜的多，但是也可以通過**誤差逆傳播演算法**（***Error BackPropagation***，**BP**）較為輕鬆地實現。   下面先用通俗的概念闡述一下什麼是誤差逆傳播演算法。誤差逆傳播演算法總體看來可以分為三個步驟，即：**前向傳播**、**反向傳播**，以及**權值更新**。 1）前向傳播：從輸入層到輸出層逐層計算出每個功能神經元的激勵函式輸出，並快取； 2）反向傳播：從輸出層到輸入層逐層計算出每個功能神經元的計算誤差，從而計算出梯度$\nabla f(w)$，這一過程需要使用在前向傳播中快取的激勵函式輸出值； 3）權值更新：按照$w^*=w-\eta\nabla f(w)$的更新規則更新權重。   下面用數學公式推導如何進行上述步驟。首先定義一些數學符號：使用下標$i$表示第$i$層，從0開始計數；$v_i$表示在前向傳播中快取的第$i$層的值，其中$v_0$表示的是輸入層的輸入；$w_i$表示第$i$層和第$i+1$層之間的權值矩陣；激勵函式為$h(v_iw_i)$。 1）前向傳播 ：參考神經元模型的計算方法，後一層的值由前一層的值和權值計算得到： $$ v_{i+1}=h(v_iw_i) $$ 2）反向傳播：以均方誤差為神經網路的代價函式，對於樣本$k$，假設輸出層為第$i+1$層，則有： $$ E_k=\frac{1}{2}(y^*_k-y_k)^T(y^*_k-y_k)=\frac{1}{2}(v_{i+1}-y_k)^T(v_{i+1}-y_k) $$   求輸出層梯度： $$ \begin{aligned} \frac{\partial E_k}{\partial w_i}&=\frac{\partial E_k}{\partial v_{i+1}}\frac{\partial v_{i+1}}{\partial v_iw_i}\frac{\partial v_iw_i}{\partial w_i}\\&=(v_{i+1}-y_k)h'(v_iw_i)v_i\\&=\delta h'(v_iw_i)v_i \\&=g_{i+1}v_i \end {aligned} $$ $$ g_{i+1}=\delta_ih'(v_iw_i)\qquad \delta_i=v_{i+1}-y_k $$   求最後一層隱藏層梯度： $$ \begin{aligned} \frac{\partial E_k}{\partial w_{i-1}}&=\frac{\partial E_k}{\partial v_i}\frac{\partial v_i}{\partial v_{i-1}w_{i-1}}\frac{\partial v_{i-1}w_{i-1}}{\partial w_{i-1}}\\&=\frac{\partial E_k}{\partial v_{i+1}}\frac{\partial v_{i+1}}{\partial v_iw_i}\frac{\partial v_iw_i}{\partial v_i}h'(v_{i-1}w_{i-1})v_{i-1}\\&=g_{i+1}w_ih'(v_{i-1}w_{i-1})v_{i-1}\\&=\delta h'(v_{i-1}w_{i-1})v_{i-1}\\&=g_iv_{i-1} \end{aligned} $$ $$ g_i=\delta_ih'(v_{i-1}w_{i-1})\qquad \delta_i=g_{i+1}w_i $$   從上述的數學公式不難總結得到一般推導公式，對於第$i$層神經元，可以計算梯度： $$ \nabla E(w_{i-1})=\frac{\partial E_k}{\partial w_{i-1}}=g_iv_{i-1}\qquad g_i=\delta_ih'(v_{i-1}w_{i-1}) $$ 這裡的$\delta_i$被定義為當前層的誤差。從前面的數學推導可以得到： （1）輸出層的誤差$\delta_i=v_i-y$，即啟用函式輸出值和真實標記的差； （2）隱藏層的誤差$\delta_i=g_{i+1}w_i$，即$g_{i+1}$與$w_i$的線性組合，係數為權值$w_i$。 3）權值更新：對於矩陣$w_i$，其更新規則如下： $$ w_i^*=w_i+\Delta w_i\qquad\Delta w_i=-\eta\frac{\partial E_k}{\partial w_i} $$ #### 四、Python實現 ##### 4.1 確定引數   這裡嘗試編寫一個高自由度可定製的多層BP神經網路。既然是高自由度，那麼先考慮可定製的引數： 1）網路規模：特徵數（輸入層神經元數）、隱藏層神經元數、類標數（輸出層神經元數），深度（權值矩陣個數，層數-1）； 2）網路學習速率：學習率、最大迭代次數； 3）激勵函式：由於是分類器，那麼輸出層的激勵函式固定為logistic較為合適，而隱藏層的激勵函式則應當可以變動。   綜上，可以得到以下引數： ```python def __init__(self, feature_n, hidden=None, label_n=2, eta=0.1, max_iter=100, activate_func="tanh"): # hidden表示隱藏層規模，即層數與每層神經元個數 pass ``` ##### 4.2 內建資料前處理器   由於要求模型能夠完成多分類任務，所以需要有一個數據前處理器來對多分類資料集類標進行獨熱編碼。這裡可以使用sklearn庫中的OneHotEncoder，而我是自己編寫了一個編碼器： ```python def _encoder(self, y): y_new = [] for yi in y: yi_new = np.zeros(self.label_n) yi_new[yi] = 1 y_new.append(yi_new) return y_new ``` ##### 4.3 資料初始化 ​ 在建構函式中初始化引數時，需要注意一下幾點： ​ 首先是隱藏層規模，隱藏層規模預設為None，在建構函式中，需要對hidden進行處理，防止使用者在未輸入hidden引數時模型接收到的隱藏層規模為None。處理方法如下： ```python if not hidden: self.hidden = [10] else: self.hidden = hidden ``` ​ 然後是啟用函式及其導數函式的引用。定義好啟用函式及其導數函式後，將其引用儲存在一個字典中，通過超參"activate_func"獲取： ```python # 函式字典 funcs = { "sigmoid": (self._sigmoid, self._dsigmoid), "tanh": (self._tanh, self._dtanh), "relu": (self._relu, self._drelu) } # 獲取啟用函式及其導數 self.activate_func, self.dacticate_func = funcs[activate_func] ``` ​ 下一步需要定義神經網路前向傳播和反向傳播過程中的重要資料結構： ```python # 擬合快取 self.W = [] # 權重 self.g = list(range(self.deep)) # 梯度 self.v = [] # 神經元輸出值 ``` ​ 最後初始化權重矩陣： ```python for d in range(self.deep): if d == 0: self.W.append(np.random.random([self.hidden[d], feature_n])) elif d == self.deep - 1: self.W.append(np.random.random([label_n, self.hidden[d - 1]])) else: self.W.append(np.random.random([self.hidden[d], self.hidden[d - 1]])) ``` ##### 4.4 BP演算法 ​ 先實現BP演算法的第一部分：前向傳播。 ```python def _forward_propagation(self, x): # 前向傳播 self.v.clear() value = None for d in range(self.deep): if d == 0: value = self.activate_func(self._linear_input(x, d)) elif d == self.deep - 1: value = self._sigmoid(self._linear_input(self.v[d - 1], d)) else: value = self.activate_func(self._linear_input(self.v[d - 1], d)) self.v.append(value) return value ``` ​ 前向傳播實現後需要實現反向傳播，完全按照數學推導的公式編寫即可： ```python def _back_propagation(self, y): # 反向傳播 for d in range(self.deep - 1, -1, -1): if d == self.deep - 1: self.g[d] = (y - self.v[d]) * self._dsigmoid(self.v[d]) else: self.g[d] = self.g[d + 1] @ self.W[d + 1] * self.dacticate_func(self.v[d]) ```   最後便可以實現完整的BP演算法和訓練演算法： ```python def _bp(self, X, y): for i in range(self.max_iter): for x, yi in zip(X, y): self._forward_propagation(x) # 前向傳播 self._back_propagation(yi) # 反向傳播 # 更新權重 for d in range(self.deep): if d == 0: self.W[d] += self.g[d].reshape(-1, 1) @ x.reshape(1, -1) * self.eta else: self.W[d] += self.g[d].reshape(-1, 1) @ self.v[d - 1].reshape(1, -1) * self.eta def fit(self, X, y): y = self._encoder(y) self._bp(X, y) return self ``` ##### 4.6 預測類標 ​ 這一過程實現很簡單，程式碼如下： ```python def _predict(self, x): y_c = self._forward_propagation(x) return np.argmax(y_c) def predict(self, X): y = [] for x in X: y.append(self._predict(x)) return np.array(y) ``` #### 五、測試模型 ##### 5.1 求解異或問題   下面用上面編寫的神經網路模型求解異或問題： ```python from model.model_demo import simple_data from model.model_demo import demo xor = simple_data("xor") demo(MLPClassifier(2, label_n=2, activate_func="tanh", max_iter=500), xor, split=False, scaler=False) ``` ​ 以下是結果：

可以看見，分類效果還是很不錯的。 ##### 5.2 求解多分類問題   這裡匯入鳶尾花資料集來測試模型進行多分類任務的效能： ```python # 求解多分類問題 from model.model_demo import iris_data from model.model_demo import demo iris = iris_data(3) demo(MLPClassifier(4, hidden=[10, 10], label_n=3, activate_func="relu", max_iter=2000), iris) ``` 結果如下： 效果