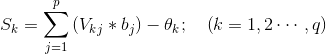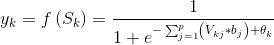人工神經網路——【BP】反向傳播演算法證明
第一步:前向傳播
【注】此BP演算法的證明僅限sigmoid啟用函式情況。本博文講道理是沒錯的,畢竟最後還利用程式碼還核對了一次理論證明結果。
關於更為嚴謹的BP證明,即嚴格通過上下標證明BP的部落格請戳這裡
簡單的三層網路結構如下
引數定義:
可見層定義為X,共有n個單元,下標用 i表示
隱藏層定義為B,共有p個單元,下標用 j 表示
輸出層定義為Y,共有q個單元,下標用 k表示
可見層到隱藏層權重矩陣為W,大小為 p*n
隱藏層到輸出層權重矩陣為V,大小為q*p
① 計算隱藏層各神經元啟用值

②計算隱含層單元的輸出值
採用sigmoid函式即S型函式
③計算輸出層各神經元啟用值
④計算輸出層單元的輸出值
第二步:逆向傳播
校正是從後往前進行的,所以稱為誤差逆傳播,計算是從輸出層到隱藏層,再從隱藏層到輸入層。更新的是權重和偏置,稱為模型引數
兩層的權重和偏置的更新是類似的,下面以輸出層到隱藏層的權重和偏置更新為例。
採用平方和誤差衡量期望輸出與實際輸出的差別:
輸出層→隱藏層的更新
先對權重求梯度:
【注】上式中最後一個等號左邊第二項求導利用對sigmoid函式求導
接下來對偏置求梯度
隱藏層→輸入層的更新
【注】建議這一層的更新,讀者認真推導,這樣會對BP的更新有更深刻的印象
第四步:模型引數校正
這一步就非常簡單啦,直接用原始的模型引數,減去現在的模型引數就行啦,其中會加入一個學習率η,控制梯度下降速度
第五步:一般性推導
【注】以下純為個人理解,與網路上那些複雜點的公式可能有出入,實際情況有待考證..............
上面只是三層BP神經網路的推導,看著已經很複雜了,這時候會產生一個想法:如果是很多層的BP神經網路該如何去推導?難道是每一層都得從最後一層挨個朝前推導一次?這時候就得考察我們的歸納能力。這裡有一個題外話,何為歸納?何為演繹?簡單點,歸納就是從特殊性到一般性,而演繹則是從一般到特殊。當然內中道理還有很多,就不說了。
如何去歸納,這裡就得說到BP中經常遇到的一個詞語:鏈式求導。如果不知道具體定義也沒事,朝下看:
①從最後一個權重開始看:這個權重連線了中間隱層和最後的輸出層,求導過程是對輸出層的sigmoid啟用函式求導,然後進一步得到的結果是:輸出誤差*輸出值*(1-輸出值)*(隱層值),換個方法說:權重右邊的輸出誤差*權重右邊的輸出*(1-權重右邊的輸出)*(權重左邊的輸出);——分割線——權重連線的右邊層的偏置更新就是去掉權重更新中乘以的權重左端值的那一引數(即權重連線的左層單元的值)。
②然後看倒數第二個權重:這個權重連線了原始輸出層和中間隱層,求導過程還是對輸出層的sigmoid啟用函式求導,只不過求導物件是第二個權重,而不是①中的權重。接下來發現不好求導,需要按照求導法則變換,變成了最後的輸出層對隱層的輸出求導乘以隱層輸出對第二個權重的求導,可以發現這兩個都好求,因為他們都直接存在與被求導的啟用函式(也就是分母的表示式)中。然後發現輸出層關於第二層權重的導數變成了:權重右邊某種值*權重右邊的輸出*(1-權重右邊的輸出)*(權重左邊的輸出)。發現與①很相似,只不過第一項有差別,然後觀察何為“權重右邊某式”,發現就是此層權重的後一層權重連線的層的偏置更新乘以連線到後一層的權重。
這樣總結出一個規律:
建立的一個BP網路如下,注意,最後的偽層只是第n層的副本,實際的BP是沒有這一層的,此處只是為了方便理解罷了,原因繼續看下去:
如圖所示,W左邊連線層A,右邊連線層B,B層的下一層是C,B和C的連線權重為V,C的偏置更新為△c,B的偏置更新為△b,則按照歸納的結論可以得到下式:
其實這裡的V是被轉置了的,因為V是從B到C的權重,那麼從C的維度到B的維度,就必須通過轉置相乘。具體涉及到矩陣求導法則,後面有部落格更新這一內容。
【注】有時候面試會經常問:權重可以初始化為零?為什麼?直接看這兩個公式就能很清晰發現是不能的,因為這兩個公式的更新都與權重有關,如果初始權重為0的時候,這兩個梯度就都是0了。
但是突然想到當A是第n-1層的時候,並沒有對應的"C"層去計算第n-1層到第n層的連線權重,也就是最後一層的權重, 那麼怎麼辦?
方法一:
我們建立了第n層資料的副本,稱為偽層,那麼此時C就是偽層了,對應的偽層偏置設定為:
對應的第n層到偽層的連線權重為主對角線為1,其它值都為0的矩陣.
這樣一來,我們可以輕鬆發現,BP的更新步驟可以用一個遞迴來解決:
步驟1:建立一個偽層副本,偽層偏置設定為△c,偽層與輸出層(第n層)的連線權重為V
步驟2:從偽層往前推,建立一個層數為3的滑動視窗,從左到右依次稱為上面介紹過的A、B、C層
步驟3:套用上面ABC更新△W和△b的方法去計算權重與偏置梯度
步驟4:返回步驟2(即往前移動一層)
步驟5:每一層的更新後引數就是
方法二:
忽視方法一種的偽層, 因為我們發現除了最後一層的所有的偏置都能用相同的公式解決,那麼我們怎麼得到最後一層的偏置?簡單,直接軲轆上一節看《輸出層→隱藏層的更新》這一節, 記住最後一層,也就是輸出層的偏置更新, 然後再去套那個三層的通用公式就OK了
【注】最近看了一個關於殘差項的博文:https://zhuanlan.zhihu.com/p/27664917,感覺文章的殘差項其實就是這裡的偏置變化量,然後在這個部落格的基礎上繼續推導(每層輸出相對於啟用函式的導數)就能得到我們的式子咯。所以本部落格的結論(ABC三層遞迴求解)是無問題的
關於從sigmoid啟用的三層BP到任意啟用函式的三層BP到任意啟用函式任意層的BP的證明請移步這裡
驗證
說了這麼多公式,還是一句話說得好: no can no bb, show me your code →__→
那麼,就扒一扒matlab的deep learning toolbox裡面的BP程式碼,以sigmoid為例,對照第五步的那個三層遞推公式看:
偽層的建立其實就是鏈式求導的開端,偽層的△c就是那個減法公式:
nn.e = y - nn.a{n};然後推匯出最後一層的△c:
switch nn.output
case 'sigm'
d{n} = - nn.e .* (nn.a{n} .* (1 - nn.a{n}));
case {'softmax','linear'}
d{n} = - nn.e;
end然後從倒數第二層開始
for i = (n - 1) : -1 : 2計算我們的ABC三層推導中的B(1-B):
switch nn.activation_function
case 'sigm'
d_act = nn.a{i} .* (1 - nn.a{i});
case 'tanh_opt'
d_act = 1.7159 * 2/3 * (1 - 1/(1.7159)^2 * nn.a{i}.^2);
end隨後計算△c*V*B(1-B),也就是當前層的偏置更新量△b:
if i+1==n % in this case in d{n} there is not the bias term to be removed
d{i} = (d{i + 1} * nn.W{i} + sparsityError) .* d_act; % Bishop (5.56)
else % in this case in d{i} the bias term has to be removed
d{i} = (d{i + 1}(:,2:end) * nn.W{i} + sparsityError) .* d_act;
end至此上一層迴圈結束,計算得到了當前層的偏置更新量。
對於權重,可以發現是△c*V*B(1-B)*A,其實就是△b乘以當前層的上一層輸出就行了,直接在最後單獨開啟新的迴圈乘一下就行了:
for i = 1 : (n - 1)
if i+1==n
nn.dW{i} = (d{i + 1}' * nn.a{i}) / size(d{i + 1}, 1);
else
nn.dW{i} = (d{i + 1}(:,2:end)' * nn.a{i}) / size(d{i + 1}, 1);
end
end附錄:引數調整方法
以下摘自【模式識別與智慧計算——MATLAB技術實現】
梯度下降法
有動量的梯度下降法
有自適應lr的梯度下降法
有動量加自適應lr的梯度下降法
彈性梯度下降法
Fletcher-Reeves共軛梯度法
Polak-Ribiere共軛梯度法
Powell-Beale共軛梯度法
量化共軛梯度法
三層BP神經網路學習的過程:
①輸入模式順傳播(輸入模型由輸入層經隱藏層向輸出層傳播)
②輸出誤差逆傳播(輸出的誤差由輸出層經隱含層傳向輸入層)
③迴圈記憶訓練(模式順傳播與誤差逆傳播的計算過程反覆交替迴圈進行)
④學習結果判定(判定全域性誤差是否趨向極小值)
UFLDL中的證明:UFLDL