題目鏈接：http://www.lydsy.com/JudgeOnline/problem.php?id=2460

網上很多題目都沒說這個題目的證明，只說了貪心策略，我比較愚鈍，在大神眼裏的顯然的策略還是想證明一下才安心……所以這裏記錄一下證明過程。

貪心策略：按魔力值從大到小排序，從大往小往線性基裏插，如果成功插入新元素，就選這個，如果插不進去，就不選這個。

證明：

　　設有n個材料，每個材料的屬性值是x[1],x[2],...,x[n]，魔力值是v[1],v[2],...,v[n]，這裏假設v已經排好序，即v[1]>=v[2]>=v[3]>=...>=v[n]。

　　首先證，一定有一個最優解，包含材料1，其屬性值是x[1]，魔力值是v[1]。

　　　　假設原問題存在一個最優解 S = { t₁, t₂, ... , t_k }。其中t_i代表第t_i個物品，且t1<t2<...<tk。

　　　　　　如果t1等於1，那麽得證。

　　　　　　如果t1不等於1，那麽我們來證一定有一個元素可以被1替換下來。

　　　　　　　　考慮1為何不能加進S。因為S是線性無關的，加入1以後，S∪{1}就變得線性相關了。所以必然存在S的一個子集，它們的異或和等於x[1]。

　　　　　　　　用表達式寫出來也就是

(1)

　　　　　　　　那麽1可以把誰替換下來呢？答案是1可以把任何一個替換下來。我們不妨讓它替換下來ti，把式子變一下形，兩邊同時異或上x[ti]^x[1]，就得到了

(2)

　　　　　　　　就會發現x[ti]已經可以被線性表示出來了，而且顯然，如果不加x[1]肯定是無法線性表示出來x[ti]的（因為S是線性無關的），所以替換後的線性基跟原來是等價的。

　　　　　　　　如果不放心，我可以再重述一遍，對於原來S可以表示出來的，替換後的一定也可以表示出來，因為被替換掉的x[ti]已經可以表示出來了；對於原來S不能表示出來的，替換後的也一定表示不出來。可以用反證法證。假設有一個y，用原來的表示不出來，而用替換後的可以表示出來。那肯定是因為加入了x[1]的原因。用式子寫出來就是：

(3)

　　　　　　　　把x[1]用(1)式代換，就可以得到：

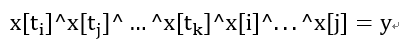(4)

　　　　　　　　是不是擔心，萬一左邊的x都抵消沒了怎麽辦？實際上不會出現這種情況，因為ti就是獨一無二的，在x[i]^...^x[j]裏是不會有的（因為ti已經被1替換下來了）。這樣，就得到了原來的基也可以得到y，與假設矛盾。

　　所以這一步證明的作用是什麽呢？就是證明了，第一步的貪心策略是正確的。下面來證明，如果第一步的貪心是正確的，以後的貪心也是正確的。

　　現在只需證，假設當前已經按照貪心策略造出了一個線性無關的基S = { t₁, t₂, ... , t_k }，一定存在一個最優解，包含下一步選擇的那個最大魔力值的跟S線性無關的一個材料。

　　設下一步的貪心策略選擇是j，假設最優解是 G = {t₁, t₂, ... , t_k , t_k+1, t_k+2, ... , t_k+m}。

　　　　如果j∈G，那麽得證。

　　　　如果j?G，現在證j一定可以替換掉G中的某個元素，實際上j可以替換掉y1,y2,...ym裏的任何一個元素，證明方法跟第一步類似。

　　　　　　j為什麽不能屬於G呢？因為G是線性無關的，但是加入j之後，就線性相關了，也就是說j是多余的，j可以用其他的線性表示出來。那麽可以得到的式子就是：

(5)

　　　　這個式子實際上跟(1)式是一模一樣的。而且這裏的i肯定>k，因為根據已知的策略，j一定會選跟t1...tk線性無關的最前面的那個。那麽到此，後面的證明跟第1步的證明也是類似的，j也可以替換掉任何一個ti (i>k)。

　　綜上，問題得證。

代碼：

#include<bits/stdc++.h>
using namespace std;

typedef long long ll;

const int maxn=1005;
pair<int,ll> a[maxn];

vector<ll> base;
bool add(ll x)
{
    for(int i=0;i<base.size();i++)
        x=min(x,x^base[i]);
    if (x) base.push_back(x);
    if (x) return true;
    else return false;
}

int main()
{
    int n;
    scanf("%d",&n);
    for (int i=0;i<n;i++) scanf("%lld%d",&a[i].second,&a[i].first);
    sort(a,a+n);
    int ans=0;
    for (int i=n-1;i>=0;i--) if (add(a[i].second)) ans+=a[i].first;
    printf("%d",ans);
    return 0;
}

[bzoj 2460]線性基+貪心