Complete space 完備空間與柯西序列 巴拿赫空間與完備空間 完備空間與和希爾伯特空間 封閉closed與完備性complete
http://www.gatsby.ucl.ac.uk/~gretton/coursefiles/RKHS2013_slides1.pdf


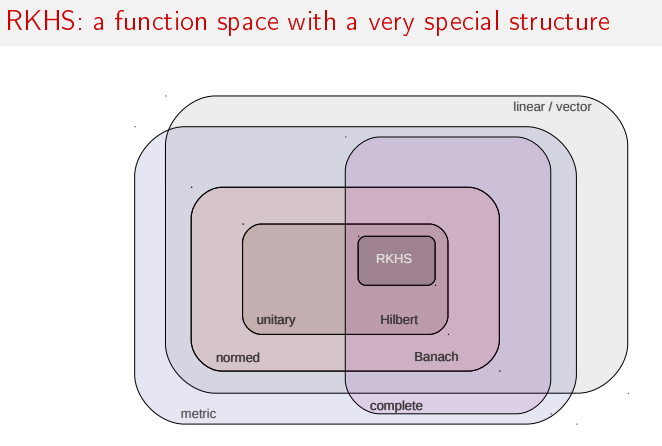
RKHS: a function space with a very special structure
Complete space 完備空間與柯西序列 巴拿赫空間與完備空間 完備空間與和希爾伯特空間 封閉closed與完備性complete
相關推薦
Complete space 完備空間與柯西序列 巴拿赫空間與完備空間 完備空間與和希爾伯特空間 封閉closed與完備性complete
sed special images ace structure des func cti str http://www.gatsby.ucl.ac.uk/~gretton/coursefiles/RKHS2013_slides1.pdf R
向量空間、賦範空間、內積空間、歐式空間、希爾伯特空間
集合 als 什麽 抽象 normal sub www. nbsp ram 一、 何為線性空間 1. 線性空間 定義:設V是一個非空集合,F為數域。如果對於任意兩個元素α、β∈V,總有唯一的一個元素γ∈V與之對應,稱為α與β的和,記作 γ=α+β 如果對於任意一個數λ∈F與
通俗理解Hilbert希爾伯特空間
著作權 以及 坐標 範數 如何 有效 answer 線段 度量 作者:qang pan 鏈接:https://www.zhihu.com/question/19967778/answer/28403912 來源:知乎 著作權歸作者所有。商業轉載請聯系作者獲得授權,非商業轉載
深刻理解空間(線性空間,度量空間,賦範空間,線性賦範空間,內積空間,巴拿赫空間以及希爾伯特空間)
在我們學習矩陣理論和統計理論的時候,總是會出現“**空間”。在之前的時候對於空間理解的過程中,總是試圖拿出一個具體的例子來加深自己的理解。但是這樣做是不對的,因為如果說對於類似“歐幾裡何空間”這樣的空間,跟我們生活中的三維空間極為相似,我們確實可以想象到一個具體的例子,但是對於類似“希爾伯特空間”之
再生核希爾伯特空間2---概念
再生核: E非空集合,H為定義在E上的複函式Hilbert空間(∀t∈E,∀ψ∈H,ψ(t)∈C),定義函式 K:E×E→C 即 K:(s,t)→K(s,t),s,t∈E
希爾伯特空間/再生核希爾伯特空間
現代數學的一個特點就是以集合為研究物件,這樣的好處就是可以將很多不同問題的本質抽象出來,變成同一個問題,當然這樣的壞處就是描述起來比較抽象,很多人就難以理解了。這裡主要整理(摘抄)了一下歐式空間和從向量空間一直到再生核希爾伯特空間的概念與簡單理解。 歐式空間/
如何理解線性賦範空間、希爾伯特空間, 巴拿赫空間,拓撲空間
賦範空間,度量空間,線性賦範空間,線性度量空間,希爾伯特空間, 巴拿赫空間,拓撲空間如何不被他們嚇到? 函式空間 一、問題的提出 在微積分中可以定義極限和連續,依賴於距離 那麼,什麼是距離呢? 通俗的看法,大家都認為距離就是所謂的直線 但
3.3.5 赫爾伯特•西蒙——…
赫爾伯特·西蒙(1916——2001)生於美國威斯康星州密爾沃基市,是20世紀文理兼通的一位科學奇才。他從研究社會科學起步,卻在政治科學、經濟學、心理學、管理科學、電腦科學和科學哲學等領域頗有建樹。從50年代開始,他把關於組織行為決策管理方面的理論應用於經濟學,還開創了人工智慧、認知科學和資訊處理心理學等新學
Python學習心得(五) random生成驗證碼、MD5加密、pickle與json的序列化和反序列化
用法 div com ict file imp randint csdn == # -*- coding:utf-8 -*- import random as rd #驗證碼 import hashlib as hsl #MD5加密 import pickle,json
MT【16】利用柯西不等式求三角的最大值
技術分享 com style img 不等式 bsp nbsp png 均值 評:此題也可以設$1+cos\theta=t$,平方後變成$t$的單變量利用均值去做. 柯西平衡系數法其實就是待定系數法,利用等號取到的條件。MT【16】利用柯西不等式求三角的最大值
MT【62】柯西求三角值域
osx $$ size use ont because left cau 解答 求$sinx(\sqrt{cos^2x+24}-cosx)$的範圍.解答:[-5,5] $$\because (sinx \sqrt{cos^2x+24}-cosxsinx)^2$$$$\le
函數式編程-函數的合成與柯裏化
word pip 滿足 鏈接 img 註意 lang num 原因 函數式編程有兩個最基本的運算:合成和柯裏化。 2.1 函數的合成 如果一個值要經過多個函數,才能變成另外一個值,就可以把所有中間步驟合並成一個函數,這叫做"函數的合成"(compose)。 上圖中,X和Y
Json與pickle資料序列化181031
json序列化 json是Python,Java等語言通用的,但是隻能序列化簡單的資料型別 # Author:Li Dongfei import json info = { "name":"dongfei", "age":"24" } f = open("test.txt","w") f.
JS函數語言程式設計 - 函式組合與柯里化
我們都知道單一職責原則,其實面向物件的SOLID中的S(SRP, Single responsibility principle)。在函式式當中每一個函式就是一個單元,同樣應該只做一件事。但是現實世界總是複雜的,當把現實世界對映到程式設計時,單一的函式就沒有太大的意義。這個時候就需要函式組合和柯里化了。 鏈
蔡高廳老師 - 高等數學閱讀筆記 - 08 - 微分中值定理 - 柯西和泰勒定理 02 -( 35、36、)
四大中值定理: 證明一:不對 柯西定理的證明 代入, a,b, 滿足羅爾定理 泰勒定理 證明: 推斷 => 有如下導數,
Go語言基礎(十四)—— Go語言切片,map,結構體與Json的序列化,反序列化
序列化和反序列化 序列化概念理解:就是將變數從記憶體中變成可儲存或傳輸的過程稱之為序列化,序列化之後,就可以把序列化後的內容寫入磁碟,或者通過網路傳輸到別的機器上。 反序列化則就是序列化反過來,把變數內容從序列化的物件重新讀到記憶體裡稱之為反序列化 序列化結構體案例: packa
《劍指offer》-- 棧的壓入與彈出序列
一、棧的壓入與彈出序列: 1、題目: 輸入兩個整數序列,第一個序列表示棧的壓入順序,請判斷第二個序列是否可能為該棧的彈出順序。 假設壓入棧的所有數字均不相等。例如序列1,2,3,4,5是某棧的壓入順
可變序列與不可變序列
直接 空間 引用 bsp 不可 nbsp 無法 可變 一個 可變類型: 比如列表:列表名(或稱為列表引用)指向堆空間中的一個列表。列表引用當中存儲的內容為地址,可以指向堆內存中的具體對象. 一方面,該列表可以保證在地址不
CRF與LSTM在序列標註問題上的不同
標註跟分類最大的區別就是:標註採的特徵裡面有上下文分類結果,這個結果你是不知道的,他在“分類”的時候是跟上下文一起"分類的"。因為你要確定這個詞的分類得先知道上一個詞的分類,所以這個得整句話的所有詞一起解,沒法一個詞一個詞解。 而分類是根據當前特徵確定當前類別,分類的時候不
