賦範空間，度量空間，線性賦範空間，線性度量空間，希爾伯特空間，巴拿赫空間，拓撲空間如何不被他們嚇到？

函式空間

在微積分中可以定義極限和連續，依賴於距離
那麼，什麼是距離呢？
通俗的看法，大家都認為距離就是所謂的直線
大航海時期的距離如何測量？
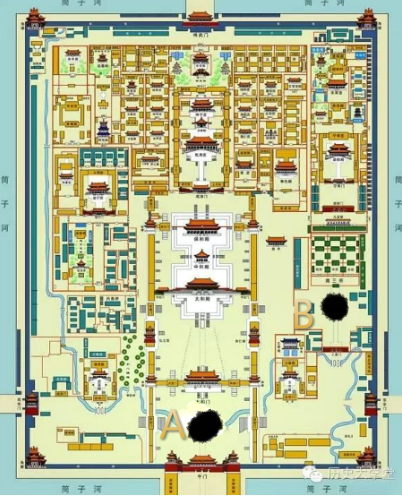
但是，在這張圖中，我們如何衡量兩點之間的距離？
因為地球儀上不能畫直線，所以這裡的距離顯然就不是直線了。我們只能沿著地球儀取曲線作為距離

再來看一張圖

從A到B的距離又是多少呢？

顯然不能計算直線距離，比較合理的距離，應該是走一個L字型（這裡就不畫出來了…）

兩個向量之間的距離又該如何定義呢？

兩條曲線之間的距離呢？

兩條曲線的距離

x=(x1,...,xn) 到 y=(y1,...,yn) 的距離

情形1：
d1(x,y)=(x1−y1)2+...+(xn−yn)2−−−−−−−−−−−−−−−−−−−−−−√
情形2：
d2(x,y)=max{|x1−y1|,...,|xn−yn|}
情形3：
d3(x,y)=|x1−y1|+|xn−yn|

其中d1是最常見的也就是中學所學的距離，而d3 則是天安門圖中從A到B的距離

曲線距離

注意這裡只能取最大值，不能取最小值。一旦取了最小值，則任意兩個有交點的曲線的距離都為0，顯然，這樣是有問題，所以只能去最大值

看了那麼多距離，我們如何定義呢？

定義距離
則稱d(x,y)是這兩點之間的距離。

定義：設

||x||是Rn的範數若滿足：
(1)||x||≥0,∀x∈Rn;||x||=0↔x=0;
(2)||αx||=|α|||x||,∀α∈R,x∈Rn;
(3)||x+y||≤||x||+||y||,∀x,y∈Rn

注意：可以簡單的看成到零點距離多了（2）；所以範數就是一個更加具體的距離！！！

我們接下來，有兩個方向可以走，一個是在距離上面加東西，讓距離更加具體化，另一種是在距離上減東西，讓距離更加抽象畫，像範數就是讓距離更加具體化了

所以範數有如下情況：

由範數可以定義距離：

d(x,y)=||x−y||
但由距離不一定可以定義範數，例如：
||x||=d(0,x),但||αx||=d(0,αx)≠|α|||x||,

所以，一旦定義了抽象的距離，我們就必須習慣用定義去證明對錯，而不能用中學的距離，來進行判斷。

賦予範數或者距離的集合分別稱為：賦範空間和度量空間
若在其上再加上線性結構稱為：線性賦範空間和線性度量空間

那麼，我們日常生活的空間可以稱為賦範空間或者度量空間麼？
答案是否定的因為這樣的空間缺少角度的概念，從前面的定義中我們無法退出角度。所以，我們才有了接下來的內容。

賦範空間有向量的模長，即範數。但是還缺乏一個很重要的概念——兩個向量的夾角，為了克服這一缺陷，我們引入：內積
定義：

設(x,y)∈R，且滿足：
（1）對稱性；
（2）對第一變元的