深刻理解空間(線性空間,度量空間,賦範空間,線性賦範空間,內積空間,巴拿赫空間以及希爾伯特空間)
在我們學習矩陣理論和統計理論的時候,總是會出現“**空間”。在之前的時候對於空間理解的過程中,總是試圖拿出一個具體的例子來加深自己的理解。但是這樣做是不對的,因為如果說對於類似“歐幾裡何空間”這樣的空間,跟我們生活中的三維空間極為相似,我們確實可以想象到一個具體的例子,但是對於類似“希爾伯特空間”之類的,我們很難用一個具體的例項來印證。所以,“**空間”到底是個什麼東西呢?
很感謝交大王老師的公開課“數學之旅”,通俗地解釋了空間到底是個什麼東西。附上鍊接:《數學之旅》——王維克。
下面我們從簡單的距離空間開始,先理解空間是什麼。
一、距離空間(度量空間)
從初中就開始學習“距離”的概念,我們總是想到這樣一個情景:在三維座標(空間)中有兩個點(
(1)
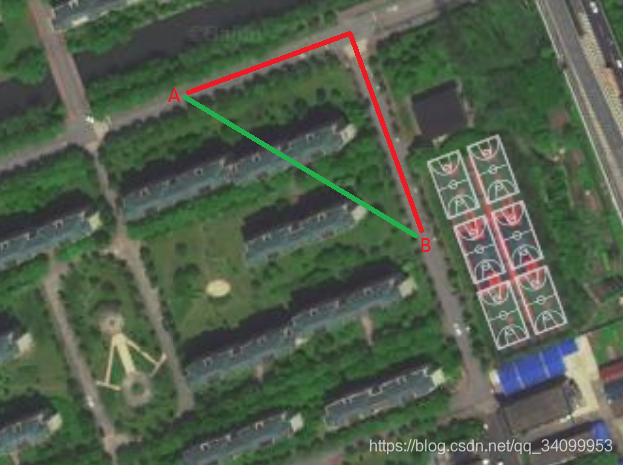
而距離所組成的空間是什麼?我們能夠用上式來理解距離空間嗎?答案是最好不要。因為距離不只有形如上式(1)的直線距離,還有航海時的球面距離,還有路徑中的折線距離等等。如下圖:實際中我們從A到B的距離是折線距離。
對於距離,我們分別可以這樣定義:
折線距離
最大距離
既然是這樣,我們應該如何去理解“距離空間”這個概念呢?為了便於理解,我們來舉另外一個例子:字典中對蘋果、水果的解釋:
| 蘋果 | 雙子葉植物,薔薇科。落葉喬木。花淡紅或淡紫紅色。大多自花不孕,需異花授粉。果實由子房和花托發育而成。果肉清脆香甜,能幫助消化。 |
| 水果 | 供食用的含水分較多的植物果實的統稱。為家庭或待客常用的果品。如梨﹑桃﹑蘋果等。 |
| 熱帶水果 |
換句話說,蘋果是一個具體的東西,因此我們可以用具體的表述來描述;而水果是一個抽象的集合,因此我們描述空間的時候,只能用其通用的屬性。類比起來,蘋果就好像是我們說的直線距離,而距離空間就是水果。這是一個抽象的東西,因此我們用這個集合中的元素所共有的屬性來定義。空間中的元素,通俗來說交空間中的點。
所以我們可以這樣來定義距離空間:
設X是非空集合,對於X中任意的兩個元素x與y,按某一法則都對應唯一的實數d(x,y),而且滿足下述三條公理:
(1)(非負性)d(x,y)≥0,[d(x,y)=0,當且僅當x=y];
(2)(對稱性)d(x,y)=d(y,x);
(3)(三角不等式)對於任意的x,y,z∈X,恆有d(x,y)≤d(x,z)+d(z,y)。
則稱d(x,y)為x與y的距離,並稱X是以d為距離的距離空間。
二、線性空間(向量空間)
線性空間即定義了數乘和加法的空間,就是具有線性結構的空間。 有了線性空間的概念之後,因為有數乘和加法,所以空間中可以找到一組基底(Basis)能夠通過線性組合得到空間中所有的點。並且滿足八項規則(交換律、結合律等)。
三、範數空間(賦範空間)
設是
的範數,滿足:
(1)(非負性)
(2)
(3)(三角不等式)對於任意的x,y,z∈X,恆有d(x,y)≤d(x,z)+d(z,y)。
我們看到,如果把範數看做到原點的距離,那麼範數空間,在距離空間的基礎上,再加一個條件。(這就好像是在水果的基礎上,再加一個條件:產於熱帶,就變成了熱帶水果)。也就是說,我們可以通過範數來定義距離,但是不能通過距離來定義範數d(x,y) = ||x-y||。
如:(1) 對應直線距離。
(2) 對應折線距離
四、線性賦範空間、線性度量空間
線性賦範空間(和線性度量空間),即是在賦範空間(和度量空間、距離空間)的基礎上,再加一個條件:線性結構。
五、內積空間
到上面為止,還不是我們所看到的空間,因為雖然範數代表了向量的長度,但是還沒有角度。所以我們需要引入角度的概念,藉助內積。
設K是實數域或複數域,H是K上線性空間,如果對H中任何兩個向量x,y,都對應著一個數(x,y)∈K,滿足條件:
1.(共軛對稱性)
2.(對第一變元的線性性)對任何x,y,z∈H及α,β∈K,有(αx+βy,z)=α(x,z)+β(y,z).
3.(正定性)對一切x∈H,有(x,x)≥0且(x,x)=0⇔x=0
到現在為止,內積空間就是我們通俗意義上所認識的空間,也叫作歐幾裡何空間(有限維的內積空間)。在這個空間上,我們可以提出向量的投影等運算。
六、巴拿赫空間和希爾伯特空間
說到這,我們再說一個概念,交完備性。也即是在取極限的時候,不會跑出去這個空間,就叫做空間的完備性。比如實數集是完備的,而有理數集是不完備的。有理數數列取極限可能是無理數。
賦範空間+完備性=巴拿赫空間
內積空間(無限維)+完備性=希爾伯特空間
換個角度來理解函式空間,如泰勒展開,是將f(x)表示為{}的線性組合的形式;比如傅立葉展開,是將f(x)表示成無限三角函式線性組合的形式。而{
}或無限維的三角函式,也叫作一個函式空間的基。
七、拓撲空間
以上都是距離或者線性空間的基礎上逐漸增加條件,那如果嘗試減少條件呢?比如不要角度的概念,甚至不要距離的概念。比如“連續”的定義:對所有的即為連續。或者寫成
。
 。
。
換句話說,拓撲是元素X與其規則合起來。所以,拓撲是弱化了的距離,能描述的範圍最廣泛。
舉例,如果距離是水果,範數是熱帶水果,那麼拓撲就是植物。
