Treeland is a country in which there are n towns connected by n - 1 two-way road such that it‘s possible to get from any town to any other town.

In Treeland there are 2k universities which are located in different towns.

Recently, the president signed the decree to connect universities by high-speed network.The Ministry of Education understood the decree in its own way and decided that it was enough to connect each university with another one by using a cable. Formally, the decree will be done!

To have the maximum sum in the budget, the Ministry decided to divide universities into pairs so that the total length of the required cable will be maximum. In other words, the total distance between universities in k pairs should be as large as possible.

Help the Ministry to find the maximum total distance. Of course, each university should be present in only one pair. Consider that all roads have the same length which is equal to 1.

The first line of the input contains two integers n and k (2 ≤ n ≤ 200 000, 1 ≤ k ≤ n / 2) — the number of towns in Treeland and the number of university pairs. Consider that towns are numbered from 1 to n

The second line contains 2k distinct integers u1, u2, ..., u2k (1 ≤ ui ≤ n) — indices of towns in which universities are located.

The next n - 1 line contains the description of roads. Each line contains the pair of integers xj and yj (1 ≤ xj, yj ≤ n), which means that the j-th road connects towns xj and yj. All of them are two-way roads. You can move from any town to any other using only these roads.

Print the maximum possible sum of distances in the division of universities into k pairs.

7 2
1 5 6 2
1 3
3 2
4 5
3 7
4 3
4 6

6

9 3
3 2 1 6 5 9
8 9
3 2
2 7
3 4
7 6
4 5
2 1
2 8

9

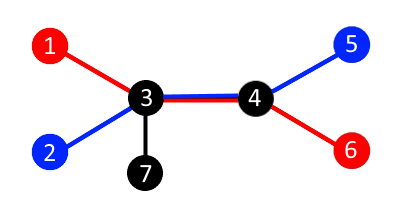
The figure below shows one of possible division into pairs in the first test. If you connect universities number 1 and 6 (marked in red) and universities number 2 and 5 (marked in blue) by using the cable, the total distance will equal 6 which will be the maximum sum in this example.

　　題目大意 給定一個邊權都為1的無向連通圖，和2k個點，將這2k個點兩兩進行配對，將每對的距離求和，問最大的距離和是多少？

　　首先看在最優的配對方案有沒有什麽規律，然而發現並沒有。

　　既然不能快速地搞定最優配對方案，那可以考慮每個點連向父節點的邊。

　　用f[i][j]表示第i個點，在第i個點的子樹內有j個點還沒有完成配對對答案的貢獻。

　　轉移是什麽？+j。這個詭異的轉移肯定有問題。

　　由於+j轉移對後面的狀態沒有什麽限制，所以開始貪心。。

　　顯然在i的子樹內沒有完成配對的點數越多越好，當然要合法，所以就將i子樹內被欽定的點數和剩余的被欽定的點數取最小值，然後直接加給答案。

Code

  1 /**
  2  * Codeforces 
  3  * Problem#400B
  4  * Accepted
  5  * Time: 62ms
  6  * Memory: 13480k
  7  */ 
  8 #include <iostream>
  9 #include <fstream>
 10 #include <sstream>
 11 #include <cstdio>
 12 #include <cstdlib>
 13 #include <cstring>
 14 #include <ctime>
 15 #include <cmath>
 16 #include <cctype>
 17 #include <algorithm>
 18 #include <map>
 19 #include <set>
 20 #include <queue>
 21 #include <stack>
 22 #include <vector>
 23 #include <bitset>
 24 #ifdef WIN32 
 25 #define Auto "%I64d"
 26 #else
 27 #define Auto "%lld"
 28 #endif
 29 using namespace std;
 30 typedef bool boolean;
 31 #define ll long long
 32 #define smin(_a, _b) _a = min(_a, _b)
 33 #define smax(_a, _b) _a = max(_a, _b)
 34 const signed int inf = (signed) (~0u >> 1);
 35 const signed ll llf = (signed ll) (~0ull >> 1);
 36 
 37 template<typename T>
 38 inline void readInteger(T& u) {
 39     static char x;
 40     while(!isdigit(x = getchar()));
 41     for(u = x - ‘0‘; isdigit(x = getchar()); u = u * 10 + x - ‘0‘);
 42 }
 43 
 44 typedef class Edge {
 45     public:
 46         int end;
 47         Edge* next;
 48         
 49         Edge(int end = 0, Edge* next = NULL):end(end), next(next) {        }
 50 }Edge;
 51 
 52 typedef class MapManager {
 53     public:
 54         int ce;
 55         Edge **h;
 56         Edge *edge;
 57         
 58         MapManager() {    }
 59         MapManager(int n, int m):ce(0) {
 60             h = new Edge*[(n + 1)];
 61             edge = new Edge[(m + 5)];
 62             memset(h, 0, sizeof(Edge*) * (n + 1));
 63         }
 64         
 65         void addEdge(int u, int v) {
 66             edge[ce] = Edge(v, h[u]);
 67             h[u] = edge + (ce++);
 68         }
 69         
 70         void addDoubleEdge(int u, int v) {
 71             addEdge(u, v);
 72             addEdge(v, u);
 73         }
 74         
 75         Edge* start(int node) {
 76             return h[node];
 77         }
 78 }MapManager;
 79 
 80 int n, m;
 81 boolean* isspy;
 82 MapManager g;
 83 
 84 inline void init() {
 85     readInteger(n);
 86     readInteger(m);
 87     m <<= 1;
 88     isspy = new boolean[(n + 1)];
 89     g = MapManager(n, 2 * n);
 90     memset(isspy, false, sizeof(boolean) * (n + 1));
 91     for(int i = 1, x; i <= m; i++) {
 92         readInteger(x);
 93         isspy[x] = true;
 94     }
 95     for(int i = 1, u, v; i < n; i++) {
 96         readInteger(u);
 97         readInteger(v);
 98         g.addDoubleEdge(u, v);
 99     }
100 }
101 
102 ll res = 0;
103 int dfs(int node, int fa) {
104     int rt = isspy[node];
105     for(Edge* it = g.start(node); it; it = it->next) {
106         if(it->end == fa)    continue;
107         rt += dfs(it->end, node);
108     }
109     res += min(m - rt, rt);
110     return rt;
111 }
112 
113 inline void solve() {
114     dfs(1, 0);
115     printf(Auto, res);
116 }
117 
118 int main() {
119     init();
120     solve();
121     return 0;    
122 }

Codeforces 700B Connecting Universities - 貪心