https://en.wikipedia.org/wiki/Modular_arithmetic#Integers_modulo_n

模算術： 整數達到特定值時會‘ 折返 ’ 回來—— 模數 modulus（moduli）

例如： 時鐘 modulo 12. 且根據定義， 12 不僅和12一致，還和0一致。

模 n 就是除數為 n 的意思。

1. 定義同余關系

　　如果 a-b=kn 那麽說 a,b 是模n同余的。n為正整數，k為整數。

　　a≡b (mod n)

　　n為同余的模數。

　　同余關系寫為： a=kn+b

　　a=pn+r

　　b=qn+r

　　r 為共同余數。0<=r<n

　　如 -8 ≡ 7 (mod 5) 2 ≡ -3 (mod 5) -3 ≡ -8 (mod 5) 商可以為負數，余數一定要為 正

　　性質1： primitive root modulo n 原根模n： 如果對於與 n互質的每一個整數 a, 都存在整數 k 使得 g^k≡a (mod n) , 則 g 為原根。

　　　　n 擁有 g 當且僅當 n=2, 4, p^k,2p^k

2. 同余類 classes

　　‘ 同余模n‘ 是一個等價關系，整數 a 的等價類為一個集合： $ \overline{\mathit{a}}_{n}=\left \{ \cdots , a-2n,a-n,a,a+n,a+2n,\cdots \right \}$

　　這個集合就是 a,n 的等價類，或殘余類。

3. 殘余系統

　　整數集合 $ \left \{ 0,1,2, \cdots , n-1 \right \} $ 被稱為 模n的最小殘余系統；

　　對於 n 個整數的集合，如果其中沒有2個同余模 n ,那麽被稱為 模n的完全殘余系統。

　　例子：

　　　　取定 n=4， 那麽 ‘ 同余類 ’ 可以為：

　　　　(1) a=1, set={ -3 ,1, 5,9,13，…} ，余數為 1

　　　　(2) a=2, set={-2, 2, 6, 10, 14, }， 余數為 2

　　　　(3) a=3, set={ -1, 3 , 7, 11, 15}， 余數為 3

　　　　(4) a=4, set={0, 4 , 8, 12, 16}， 余數為 0

　　　　從上面4個式子中各取一個元素出來，就組合成了 ‘’ 完全殘余系統‘ ； ‘其中，’ 最小殘余系統‘’ 為{1,2,3,4}

4. 約化殘余系統 RRS

　　歐拉函數 φ： 輸入為整數 n， 輸出為小於n 且與n互質的正整數個數。

　　RRS 中的元素為 φ(n) 個，它們與 n 互質，且彼此不同余！如 n=4 時， {5,15} 為 RRS

5. 整數模 n integers modulo n

　　所有 ‘ 同余類’ 的集合稱為 ‘ 整數模n的環’； 也就是說， Z/nZ 裏的元素還是集合，如3中的(1) (2) (3) (4)　, 共有n個

　　我們可以在這個環上定義加法，減法和乘法：

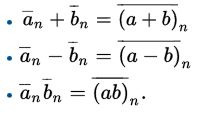
　　這些 集合 與 集合 的運算顯然是成立的。

　　例如，環 Z/24Z 中 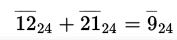因為33除以24，余數為9

　　當且僅當 n 為質數時， 這個環是個有限域。

模算術 modular arithmetic