https://www.codelast.com/math-concepts-%E6%95%B0%E5%AD%A6%E6%A6%82%E5%BF%B5/

這裏記錄了我在學習過程中遇到或總結的一些基礎數學概念，保存於此，與需要者共享。

Following are some basic math concepts I read or summarized in my learning process, I wrote them down here to share with those who need them.

（1）奇異函數

奇異函數是一種理想化的函數，它具有一個或多個間斷點，在這些點上無法確定函數或其導數值。常用的有階躍函數和沖激函數。

（2）奇點

所有不滿足整體性質的個別點，在數學上都可以稱為奇點。

如果奇點出現在分母極限為0的情況，通常來說就是產生無窮大解的表達式，在這種情況下數學計算失效。

在復變函數中，奇點的定義：若函數（復變函數）f(z)在某點z0不解析，但在z0的任一鄰域內都有f(z)的解析點，則z0稱為f(z)的奇點（singular point）。

“奇點”是復變函數裏的一個概念。在一個區域內可導的復變函數，稱為這個區域內的解析函數，如果一個復變函數在挖掉點z的區域內解析，但在點z處不解析，則z稱為這個解析函數的奇點。解析函數的奇點總是孤立的，奇點按其性質，可以分為：可去奇點、極點和本性奇點三大類。

（3）病態多項式

“病態多項式”是與病態代數方程的概念相關的。

在代數方程中，有的多項式系數有微小擾動時其根變化很大，這種根對系數變化的敏感性稱為不穩定性（instability），這種方程就是病態多項式方程。通常重根的方程是病態的，有幾個根彼此很靠近，則這些根對系數的擾動也是敏感的，有時根看起來分隔得很好，但同樣可能是病態的——這段話來自《現代應用數學手冊：計算與數值分析卷》一書。

由於在計算機數值算法中，求根過程總是通過叠代來完成的，而叠代過程又是通過一個初始解，不斷地修改這個解，最後達到某個收斂標準為止，而一個病態多項式的系數微小變化就會引起根的很大變化，因此在叠代過程中可能導致求出的根不可信。

病態多項式的一個例子：

（4）超線性收斂
如果一種方法（這裏指算法），是以前一次叠代的一階冪乘以一個小於1的因子的速度收斂，則稱這種方法為線性收斂（例如二分法），而以高階冪收斂的方法稱為超線性收斂。

具體描述：

設算法產生點列 {x(k)} ，收斂到解 x? ，且 x(k)≠x?,?k ，則

A）線性收斂： ∥∥x(k+1)?x?∥∥∥∥x(k)?x?∥∥<1 ，當 k 充分大時成立

B）超線性收斂： limk→∞∥∥x(k+1)?x?∥∥∥∥x(k)?x?∥∥=0

C）二階收斂： ?α>0 ，當 k 充分大時有： ∥∥x(k+1)?x?∥∥∥∥x(k)?x?∥∥2≤α

我們知道上面的符號||……||是範數的符號，範數可以用來度量向量之間的距離。對最簡單的情況——一維向量來說——上面的各個相減的式子就可以表示兩點之間的距離。

（5）卷積
http://www.codelast.com/?p=994

（6）最小二乘的理論依據
http://www.codelast.com/?p=1027

（7）Powell算法
http://www.codelast.com/?p=388

（8）黃金比例搜索算法
http://www.codelast.com/?p=434

（9）奇異方程組
行退化或列退化的方程組稱為奇異方程組。

（10）奇異值分解
一種處理奇異問題的方法，有時能將奇異問題轉為非奇異問題來解決。

在很長時間內，奇異值分解都無法並行處理（雖然 Google 早就有了MapReduce 等並行計算的工具，但是由於奇異值分解很難拆成不相關子運算，即使在 Google 內部以前也無法利用並行計算的優勢來分解矩陣）。

2007年初，Google 中國的張智威博士和幾個中國的工程師及實習生已經實現了奇異值分解的並行算法，這是 Google中國對世界的一個貢獻。

（11）主元
在解線性方程組時，通過加減乘除，將系數矩陣的a00，a11，a22，……（即主對角線上的元素）化為單位矩陣的形式（其他元素均化為零），在每一次計算過程中，用作除數的元素即為主元/主元素。如果計算過程中完全沒有“行交換”或“列交換”，則這種方法稱為“不選主元”的方法。

（12）完全主元法 & 部分主元法
在解線性方程組的選主元法中，如果只有行交換操作，則稱該方法為部分主元法；如果行交換和列交換操作都有，則稱該方法為完全主元法。

（13）矩陣的初等變換
a、交換矩陣的兩行（列）；

b、用一個不為零的數乘矩陣的某一行(列)；

c、用一個數乘矩陣某一行（列）加到另一行（列）上。

（14）外推法
一種 “根據已知的數值推斷已知數值範圍以外的數值” 的方法。

（15）Ridders求導算法
http://www.codelast.com/?p=1419

（16）線性/非線性規劃
第一次看到這個名詞的時候，你一定有一種它好高深的感覺，但實際上它不過是“最優化”問題的一種“特例”罷了。當最優化問題中的自變量的定義域是有限維空間中的一個子集時，這種問題就稱為線性/非線性規劃。舉個簡單的例子來說，對一個自變量為1維的函數f(x)=ax+b，自變量的定義域為（1, 9.8），它是1維空間的一個子集，那麽，通過最優化方法來求解a、b的問題，就稱為線性規劃。但是要註意，當x只能取幾個值時，例如x只能取1、5、9.8這幾個值，則這種最優化問題就不叫線性/非線性規劃了，而是叫組合優化。有時候這些界限劃分得很清晰的概念反而讓人覺得很混淆，我認為它們確實對理解問題起到了負面的作用。

平常看到的很多資料中，對這些類似的概念故弄玄虛的解釋什麽的，最讓人不舒服了！

（17）凸集
凸集在最優化領域占有重要地位。其數學定義是：設有N維空間的子集D，如果對於任意的向量（也可以說是N維空間中的點）X1，X2∈D，以及任意的實數a∈[0, 1]，都有aX1+(1-a)X2∈D，則稱D為凸集。凸集的幾何意義是：如果D為非空集合，則連接D中任意兩個點X1、X2的線段仍屬於該集合。

這似乎有點令人費解：aX1+(1-a)X2與兩點之間的連線有什麽關系呢？它表示連接這兩點的線段上的任意一點。簡單推導如下：假設X為線段X1X2上的任一點，則向量X2X（向量應該打上箭頭，但是為了書寫方便，我就省略了）平行於向量X2X1，且0≤ |X2X| ≤ |X2X1| 。因此，存在a∈[0, 1]，使得 X2X = a X2X1，即：X - X2 = a (X1 - X2)，即 X = aX1+(1-a)X2 。由於X是線段X1X2上任一點，因此前面的結論不言自明。

（18）半正定矩陣
n×n的矩陣M，若對於任意非零的x∈Rn，有xTMx≥0，則稱M為半正定矩陣。

（19）奇異矩陣
首先，一個矩陣必須是方陣，才有奇異或非奇異的概念。其次，若該矩陣的行列式為0，則其為奇異矩陣，否則就是非奇異矩陣。

可逆矩陣是非奇異矩陣，非奇異矩陣也是可逆矩陣。

（20）最速下降法/steepest descent，牛頓法/newton，共軛方向法/conjugate direction，共軛梯度法/conjugate gradient，etc.

http://www.codelast.com/?p=2573

（21）水平集

假設X∈Rn，則集合 S = {X∈Rn | f(X) ≤ a} 稱為一個水平集，其中a為常數。

（22）由兩兩線性無關的列向量構成的矩陣是滿秩的

先看wikipedia的定義，就很容易明白了：兩兩線性無關的列向量構成的矩陣必然是滿秩的。

（23）線性流形

“流形”（manifold）是數學中用於描述幾何形體的一個概念，它是指局部具有歐幾裏得空間性質的空間。 歐幾裏得空間就是最簡單的流形的實例。歐幾裏得空間也被理解為線性流形。

這個詞聽起來挺怪的，我想，要記住它，可以從表面含義來看：“流形”——流動的形狀，光滑的；“線性”——連續的。結合起來，N維歐幾裏得空間Rn就是這麽回事。

（24）滿秩與正定的一個關系

設C為滿秩矩陣，A為正定的實對稱矩陣，則CTAC是正定的。因此可推出：若C是由兩兩線性無關的向量構成的矩陣（則其為滿秩的），則CTAC正定。

（25）二次型

二次型是一些變量上的二次齊次多項式。齊次多項式是指各項的總次數均相同的多項式 ，例如 x5 + 2x3y2 + 9xy4 就是一個五次的雙變元（x和y）齊次多項式，其各項的總次數都是5。

（26）正定二次型

設有實二次型 f = XTAX，若對於任何X≠0，都有 f(X)>0，則稱 f 為正定二次型，並且稱對稱矩陣A為正定的。反之，若 f(X)<0，則稱 f 為負定二次型。

（27）正定矩陣均可逆，並且其逆也是正定矩陣

（28）柯西不等式/柯西-施瓦茨不等式/Cauchy–Schwarz inequality

相當有用的一個不等式，表達式如下：

若把這個式子寫成兩個向量u，v的形式，則為：

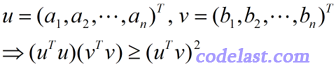
（29）大O和小o：同階無窮小與高階無窮小

大O和小o分別代表同階無窮小與高階無窮小，註意不要弄混了。例如，β與α是同階無窮小，記作β=O(α)；β是比α高階的無窮小，記作β=o(α) 。

（30）稀疏矩陣：元素大部分為0的矩陣

（31）關於正定矩陣共軛的非零向量組線性無關

（32）實對稱矩陣A正定的充分必要條件是存在可逆矩陣C，使得 A=CTC。由於可逆矩陣是正定矩陣，所以對稱正定矩陣A滿足：存在正定矩陣D，使得A=DTD

（33）每一個秩一矩陣都可以化為一個列向量與一個行向量之積

例如A為n×n的秩一矩陣，則存在n×1向量u，v，使得A=uvT

（34）駐點及鞍點

駐點：一階導數為0的點。它包括3種類型：極小點、極大點、鞍點。

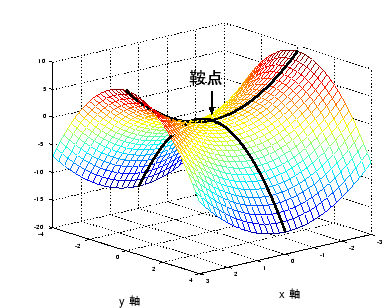
鞍點：沿某些方向是極小點；沿另一些方向是極大點，這樣的點稱為鞍點。想像一下馬鞍的形狀：馬鞍凹下去的那部分的最低點，就是鞍點的一個例子（圖片來源於網絡，感謝原作者）：

（35）雅可比矩陣（Jacobi matrix）不一定是方陣（n×n的矩陣）

（36）無解的線性方程組被稱為是不相容的，有一或無窮多個解的線性方程組被稱為是相容的

（37）若一個矩陣經過一系列行初等變換可以變成另一個矩陣，則稱這兩個矩陣是行等價的

（38）一元二次方程 ax2+bx+c=0(a≠0) 的求根公式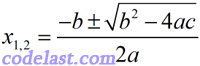

Math concepts / 數學概念(轉)