編譯：李雷、張馨月、王夢澤、小魚

除了文中所附的代碼塊，你也可以在文末找到整個程序在Jupyter Notebook上的鏈接。

在數據科學或統計學領域的眾多話題當中，我覺得既有趣但又難理解的一個就是貝葉斯分析。在一個課程中，我有機會學習了貝葉斯統計分析，但我還需要對它做一些回顧和強化。

從個人觀點出發，我就是想更好地理解貝葉斯理論，以及如何將它應用於現實生活中。

本文主要是受到了RasmusB??th在Youtube上的系列節目“貝葉斯數據分析入門”的啟發。RasmusB??th非常善於讓你直觀地理解貝葉斯分析，不是拋各種復雜的公式給你，而是引導你一步步去思考。

RasmusB??th的視頻鏈接：

https://www.youtube.com/user/rasmusab/feed

本文將通過貝葉斯理論來分析棒球選手的命中率，手把手教你如何利用貝葉斯理論進行分析。說實話，我不是一個體育迷，也很少看體育比賽。

那麽為什麽選擇棒球？

“不論你了解與否，但棒球的魅力就在於精確度。沒有其他運動像棒球這樣完全依賴於運動數據的連續性，統計性和有序性。棒球球迷比註冊會計師還要關註數字。”

——體育記者Jim Murray

有人說棒球可能是世界上數據記錄得最詳細的運動。歷史上已經累積了近百年來的棒球統計數據。

然而，僅僅收集統計數據並不會讓棒球在統計方面變得有趣，也許更重要的是這項運動本身的特點。

舉例來說，在完成一次打數(At Bats，是棒球運動中的一個成績計算名詞，指擊球手完成打擊的次數)過程中，誰在外野打球對於擊球手是否可以擊中本壘打影響甚微。

在其他體育運動，尤其是足球和籃球運動中，球員統計數據的意義可能會因球場內其他地方發生的重要事件而被淡化。而棒球這項運動中，統計數據在比較球員表現上發揮了重要作用。

棒球統計數據包含很多指標，有些指標的定義很直觀，有些則比較復雜。我選擇觀察的測量指標是打擊率 (Batting Average，AVG)。在棒球中，打擊率由安打（Hits，安打是棒球運動中的一個名詞）次數除以打數來定義，通常精確到小數點後三位。

有人質疑打擊率的作用，但正如C. Trent Rosecrans所說，“盡管如此，打擊率相較於其他統計數據而言確實是有歷史和背景意義。我們都知道AVG為0.300打者的水平怎麽樣，我們也知道AVG為0.200打者有多糟，以及AVG為0.400打者有多棒。”

在美國職業棒球大聯盟(MLB)中，春季訓練是在常規賽季開始之前的一系列練習和表演賽。

我會嘗試解決以下兩個問題：

如何解讀2018年春季訓練中的打擊率

怎麽比較兩名球員的打擊率

在進入代碼內容之前，我會簡要介紹一下Rasmus B??th在他的視頻中所講的內容。

首先，我們需要三樣東西來完成貝葉斯分析。

1.數據

2.生成模型

3.先驗概率

就我的例子而言，數據就是我們所觀察到的2018年春季訓練的打擊率。

生成模型就是當給定參數作為輸入時生成數據的模型。這些輸入參數用於生成一個概率分布。例如，如果知道平均值和標準差，則可以通過運行以下代碼輕松生成所選數據集的正態分布數據。稍後我們會看到其他類型的分布在貝葉斯分析中的運用。

import matplotlib.pyplot as pltimport numpy as npmu, sigma = 0, 0.1 # mean and standard deviations = np.random.normal(mu, sigma, 1000)plt.hist(s)

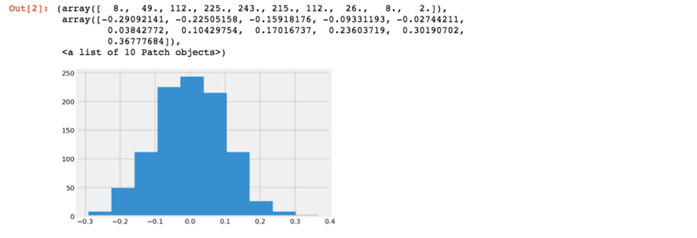
就貝葉斯分析而言，我們會逆向生成模型並嘗試用觀測數據推斷參數。

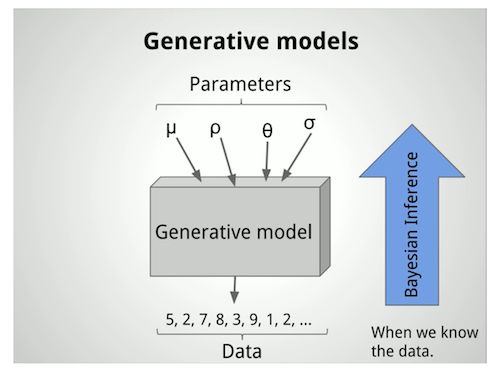
貝葉斯數據分析簡介第1部分

最後，先驗概率是指模型在處理數據之前就已有的信息。比如，事件是否等概率？是否有一些先前的數據可以利用？是否可以做出有依據的推測？

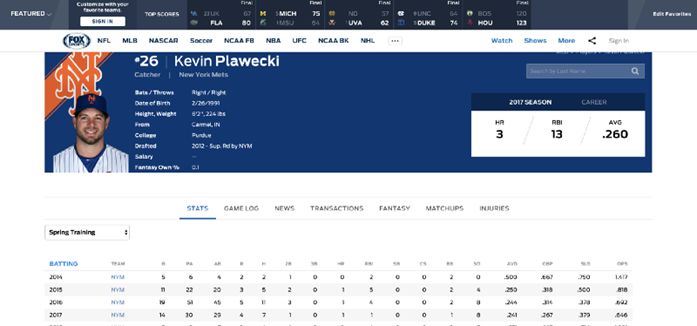
首先我將定義一個從Fox Sports抓取球員數據的函數，然後抓取球員的春季訓練或常規賽季的擊球統計數據。

Fox Sports鏈接：

https://www.foxsports.com/mlb/stats

import pandas as pdimport seaborn as snsimport requestsfrom bs4 import BeautifulSoupplt.style.use(‘fivethirtyeight‘)%matplotlib inline%config InlineBackend.figure_format = ‘retina‘def batting_stats(url,season): r = requests.get(url) soup = BeautifulSoup(r.text, ‘lxml‘) table = soup.find_all("table",{"class": "wisbb_standardTable tablesorter"})[0] table_head = soup.find_all("thead",{"class": "wisbb_tableHeader"})[0]if season == ‘spring‘: row_height = len(table.find_all(‘tr‘)[:-1])else: row_height = len(table.find_all(‘tr‘)[:-2]) result_df = pd.DataFrame(columns=[row.text.strip() for row in table_head.find_all(‘th‘)], index = range(0,row_height))

row_marker = 0for row in table.find_all(‘tr‘)[:-1]: column_marker = 0 columns = row.find_all(‘td‘)for column in columns: result_df.iat[row_marker,column_marker] = column.text.strip() column_marker += 1 row_marker += 1return result_df

接著，我們選擇一個感興趣的球員，並對其統計數據進行分析。

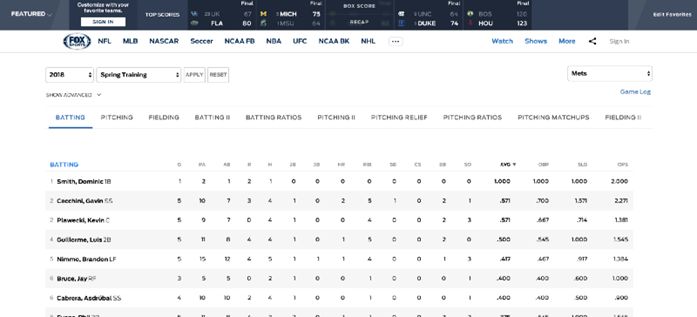
紐約大都會隊春季訓練的統計頁面

如果按照球員的打擊率（AVG）排列，你可以看到第一名是Dominic Smith（DS），而Gavin Cecchini（GC）則排第二。那他們是優秀球員嗎？我不知道。但如果僅看AVG，DS以1.000的AVG 值位於榜首。

在谷歌上搜了一下，我發現“近年來，全聯盟的平均擊打率通常在0.260左右”。如果是這樣，那麽DS和GC的AVG似乎太高了。通過進一步觀察兩位選手的打數（AB）和安打（H），顯然DS只有1個AB而GC有7個。並且在查看其他選手的AB後發現，2018年最高的AB為13，而2017年紐約大都會隊的最高AB為60。

場景一

假設我對球員們過去的表現一無所知，2018年春季訓練是唯一的數據來源，因此我不並知道AVG的取值範圍。那麽，我應該如何解讀2018年春季訓練的統計數據？

首先我們來抓取DS的春季訓練數據。

ds_url_st = "https://www.foxsports.com/mlb/dominic-smith-player-stats?seasonType=3"dominic_smith_spring = batting_stats(ds_url_st,‘spring‘)dominic_smith_spring.iloc[-1]

n_draw = 20000prior_ni = pd.Series(np.random.uniform(0, 1, size = n_draw))plt.figure(figsize=(8,5))plt.hist(prior_ni)plt.title(‘Uniform distribution(0,1)‘)plt.xlabel(‘Prior on AVG‘)plt.ylabel(‘Frequency‘)

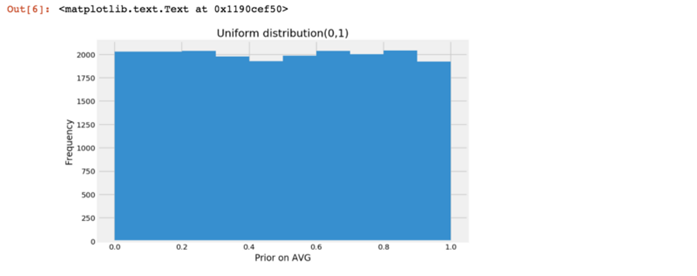
先驗概率代表了我們在得到具體數據之前對某事物的普遍看法。在上述分布中，所有概率幾乎相同（由於是隨機生成，所以存在輕微差異）。

因此，這意味著我對球員一無所知，甚至無法對AVG做任何合理的猜測。我假設AVG是0.000和AVG是1.000的概率相同，或者等於AVG值為0和1之間任何數值的概率。

現在我們觀察到的數據表明當有1個AB和1個H時，AVG是1.000，這可以用二項分布來表示。具有二項式分布的隨機變量X表示在n次獨立的是/非試驗序列中成功的次數，其中每次試驗成功的概率是p。

在我們的例子裏，AVG是成功的概率，AB是試驗次數，H是成功次數。

先記住這些術語，然後我們來定義逆向生成模型。

我們將從定義的均勻分布中隨機選取一個概率值，並將此概率用作生成模型的參數。假設我們隨機挑選的概率值為0.230，這意味著在二項分布中成功的概率為23％。

試驗次數為1（DS有1個AB），如果生成模型的結果與我們觀察到的結果相匹配（DS有1個H），那麽概率值為0.230保持不變。如果我們重復這個過程並進行過濾，最終將得到一個概率分布，由它所得到的結果與我們觀察到的結果相同。

這就是後驗概率。

def posterior(n_try, k_success, prior): hit = list()for p in prior: hit.append(np.random.binomial(n_try, p)) posterior = prior[list(map(lambda x: x == k_success, hit))] plt.figure(figsize=(8,5)) plt.hist(posterior) plt.title(‘Posterior distribution‘) plt.xlabel(‘Posterior on AVG‘) plt.ylabel(‘Frequency‘) print(‘Number of draws left: %d, Posterior mean: %.3f, Posterior median: %.3f, Posterior 95%% quantile interval: %.3f-%.3f‘ % (len(posterior), posterior.mean(), posterior.median(), posterior.quantile(.025), posterior.quantile(.975)))ds_n_trials = int(dominic_smith_spring[[‘AB‘,‘H‘]].iloc[-1][0])ds_k_success = int(dominic_smith_spring[[‘AB‘,‘H‘]].iloc[-1][1])posterior(ds_n_trials, ds_k_success, prior_ni)

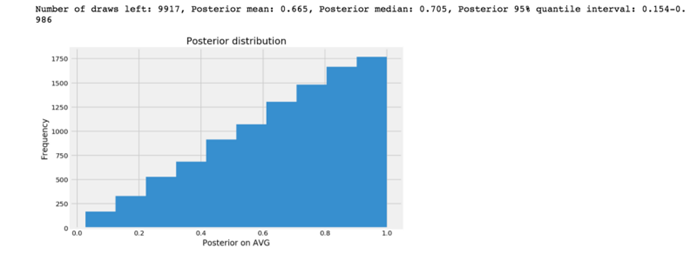
後驗概率分布中95％的分位數區間稱為可信區間，這與頻率統計中的置信區間略有不同。還有另一種可以使用的可信區間，我後面講到Pymc3時會提到。

貝葉斯統計中的可信區間和頻率統計的置信區間的主要區別是二者的釋義不同。貝葉斯概率反映了人的主觀信念。根據這種理論，我們可以認為真實參數處於可信區間內的概率是可測量的。這種說法很吸引人，因為它使我們能夠直接用概率對參數進行描述。

許多人認為這個概念是理解概率區間的一種更自然地方式，也很容易解釋。置信區間使你能判斷某區間是否包含真實的參數。

如果我們收集一個新樣本，計算置信區間，並多次重復這個過程，那麽我們計算出的95％的置信區間將包含真實的AVG值。

可信區間：根據觀察數據，AVG的真實值落在可信區間內的概率為95％。

置信區間：當我們用這類數據計算置信區間時，有95%的置信區間會包含AVG的真實值。

註意兩者的區別，可信區間是在給定固定邊界情況下對參數值的概率描述，置信區間是在給定固定參數值情況下的邊界概率。

在現實生活中，我們想知道的是真實的參數而不是邊界，因此，貝葉斯可信區間是更合適的選擇。在這種情況下，我們只對球員的真實AVG感興趣。

有了上面的後驗分布，我有95%的把握斷定DS真正的AVG將在0.155到0.987之間。但這個範圍太大了。換句話說，在沒有先驗知識並且在只觀察了一次試驗的情況下，我不太確定DS的真實AVG是多少。

場景二

對於第二個場景，我們假設知道上一年的春季訓練的統計數據。

dominic_smith_spring.iloc[-2:]

現在我們有了2017年春季訓練的統計數據，我們的先驗假設應該反映這方面的信息。註意到2017年春季訓練時DS的AVG是0.167，因此2017年的統計數據不呈均勻分布。

Beta分布是一個連續概率分布，它有兩個參數，alpha和beta。Beta分布最常見的用途之一是對一個實驗的成功概率的不確定性進行建模。

特別地，在已知n次試驗中觀察到k次成功的條件下，X的條件分布是一個alpha=k+1、beta=n- k+1的Beta分布。

Beta分布相關內容：

https://www.statlect.com/probability-distributions/beta-distribution

n_draw = 20000prior_trials = int(dominic_smith_spring.iloc[3].AB)prior_success = int(dominic_smith_spring.iloc[3].H)prior_i = pd.Series(np.random.beta(prior_success+1, prior_trials-prior_success+1, size = n_draw))plt.figure(figsize=(8,5))plt.hist(prior_i)plt.title(‘Beta distribution(a=%d, b=%d)‘ % (prior_success+1,prior_trials-prior_success+1))plt.xlabel(‘Prior on AVG‘)plt.ylabel(‘Frequency‘)

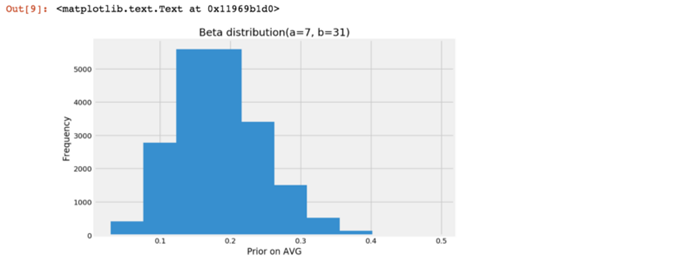
posterior(ds_n_trials, ds_k_success, prior_i)

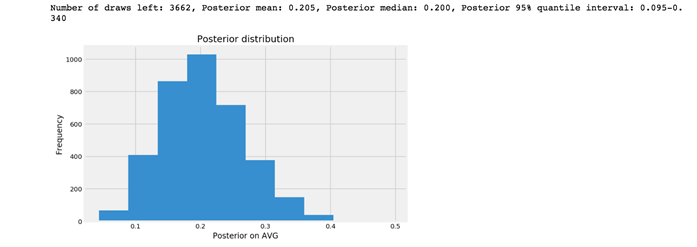
和在場景一中使用均勻分布的先驗假設得到的後驗結果相比，這裏95%的分位數區域已經被縮小了。現在我有95%的把握斷定DS的AVG會在0.095到0.340之間。

然而，一般來說AVG超過0.300已經是優秀的打者了，這裏對AVG的估計意味著這名球員可以是最差或是最好的打者。所以我們需要更多的數據來縮小可信區間的範圍。

場景三

在這個場景中，假設我不僅有2017年春季訓練的統計數據，還有2017年常規賽的統計數據。那麽這會如何影響後驗結果和結論呢?

ds_url = "https://www.foxsports.com/mlb/dominic-smith-player-stats?seasonType=1"dominic_smith_reg = batting_stats(ds_url,‘regular‘)dominic_smith = dominic_smith_reg.append(dominic_smith_spring.iloc[3], ignore_index=True)dominic_smith

ds_prior_trials = pd.to_numeric(dominic_smith.AB).sum()ds_prior_success = pd.to_numeric(dominic_smith.H).sum()n_draw = 20000prior_i_02 = pd.Series(np.random.beta(ds_prior_success+1, ds_prior_trials-ds_prior_success+1, size = n_draw))plt.figure(figsize=(8,5))plt.hist(prior_i_02)plt.title(‘Beta distribution(a=%d, b=%d)‘ % (ds_prior_success+1,ds_prior_trials-ds_prior_success+1))plt.xlabel(‘Prior on AVG‘)plt.ylabel(‘Frequency‘)

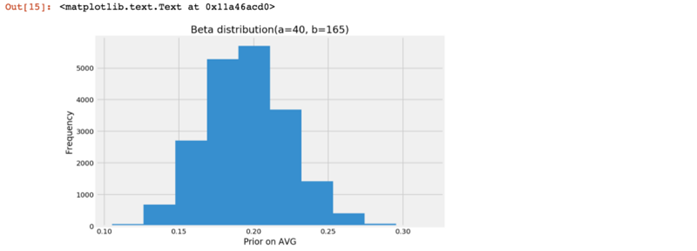
posterior(ds_n_trials, ds_k_success, prior_i_02)

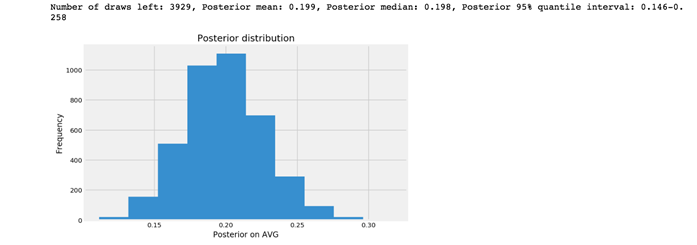
現在我有95%的把握斷定DS的真正AVG將在0.146到0.258之間。雖然範圍不是很精確，但與場景一和場景二相比，場景三的可信區間要窄得多。

場景四

我想比較兩名選手，看看誰在AVG方面表現得更好。我觀察的數據來自2018年春季訓練，先驗知識是2017年的春季訓練和常規賽。現在我要比較DS和GC這兩名選手的打擊率。

在場景三中，我剔除了所有生成的結果與觀察數據不一致的參數，然後進行模擬采樣。但是這種類型的隨機樣本生成和過濾計算量很大，並且運行緩慢。

因此，我們可以借助一些工具使采樣器在高概率的區域花費更多的時間以提高效率。像Pymc3這樣的概率編程工具可以通過使用諸如HMC-NUTS之類的巧妙算法來有效地處理采樣過程。

Pymc3鏈接：

https://github.com/pymc-devs/pymc3

HMC-NUTS鏈接：

http://blog.fastforwardlabs.com/2017/01/30/the-algorithms-behind-probabilistic-programming.html

我們先從Fox Sports中抓取Gavin Cecchini的統計數據。

gc_url_st = "https://www.foxsports.com/mlb/gavin-cecchini-player-stats?seasonType=3"gc_url_reg = "https://www.foxsports.com/mlb/gavin-cecchini-player-stats?seasonType=1"gavin_cecchini_spring = batting_stats(gc_url_st,‘spring‘)gavin_cecchini_reg = batting_stats(gc_url_reg,‘regular‘)gc_n_trials = int(gavin_cecchini_spring.iloc[1].AB)gc_k_success = int(gavin_cecchini_spring.iloc[1].H)gc_prior = pd.DataFrame(gavin_cecchini_reg.iloc[1]).transpose().append(gavin_cecchini_spring.iloc[0])gc_prior

gc_prior_trials = pd.to_numeric(gc_prior.AB).sum()gc_prior_success = pd.to_numeric(gc_prior.H).sum()def observed_data_generator(n_try,observed_data): result = np.ones(observed_data) fails = n_try - observed_data result = np.append(result, np.zeros(fails))return resultds_observed = observed_data_generator(ds_n_trials,ds_k_success)gc_observed = observed_data_generator(gc_n_trials,gc_k_success)

接著，我們擬合一個Pymc3模型。

import pymc3 as pmwith pm.Model() as model_a: D_p = pm.Beta(‘DS_AVG‘, ds_prior_success+1, ds_prior_trials-ds_prior_success+1) G_p = pm.Beta(‘GC_AVG‘, gc_prior_success+1, gc_prior_trials-gc_prior_success+1) DS = pm.Bernoulli(‘DS‘, p=D_p, observed=ds_observed) GC = pm.Bernoulli(‘GC‘, p=G_p, observed=gc_observed) DvG = pm.Deterministic(‘DvG‘, D_p - G_p) start = pm.find_MAP() trace = pm.sample(10000, start=start)pm.plot_posterior(trace, varnames=[‘DS_AVG‘,‘GC_AVG‘,‘DvG‘],ref_val=0)

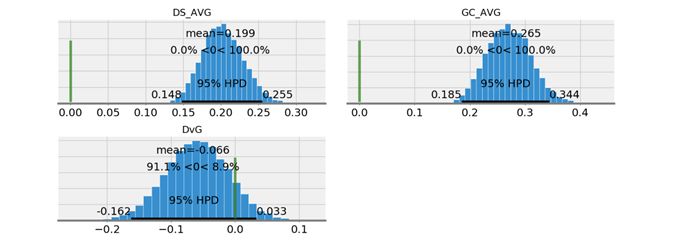
如果我們用Pymc3中的plot_posterior函數繪制DS_AVG、GC_AVG和DvG (DS_AVG - GC_AVG)的後驗分布，我們可以看到圖中出現的術語是HPD而不是分位數（quantile）。

最大後驗密度（Highest Posterior Density，HPD）區間是我們可以對後驗密度函數使用的另一種可信區間。HPD區間會選擇包括眾數在內的最大後驗概率密度值所在的最窄區間。

在Rasmus B??th的另一篇文章中，比較了分位數區間和最高密度區間，並提供了簡單明晰的對比圖。以下是六種不同後驗分布中的眾數和覆蓋了95%的概率密度的最高密度區間。

文章鏈接：

http://www.sumsar.net/blog/2014/10/probable-points-and-credible-intervals-part-one/

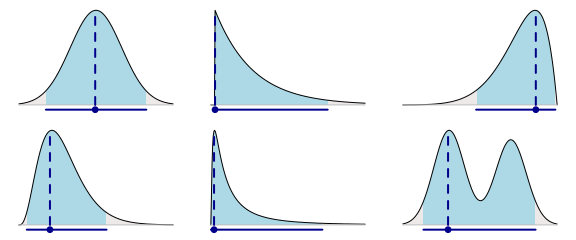
可能的點和可信區間，第1部分：圖形總結

分位數區間包含中位數，中位數落在區間左側的概率是50%，落在右側的概率也是50%，同時以95%的可信區間為例，落在區間任意一側的概率是2.5%。

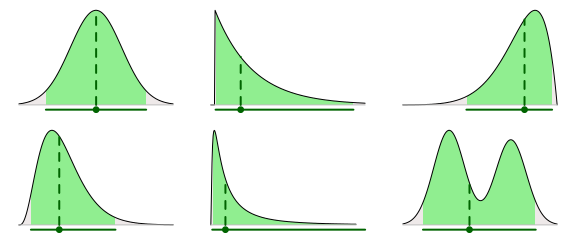
可能的點和可信區間，第1部分:圖形總結

就DS和GC的AVG來看，它們的眾數和中位數看起來並沒有多大區別，若實際情況確實如此，兩位選手AVG的HPD區間和分位數區間應該也大致相同。讓我們看看它們到底長什麽樣。

pm.summary(tracehuarenyl.cn/)

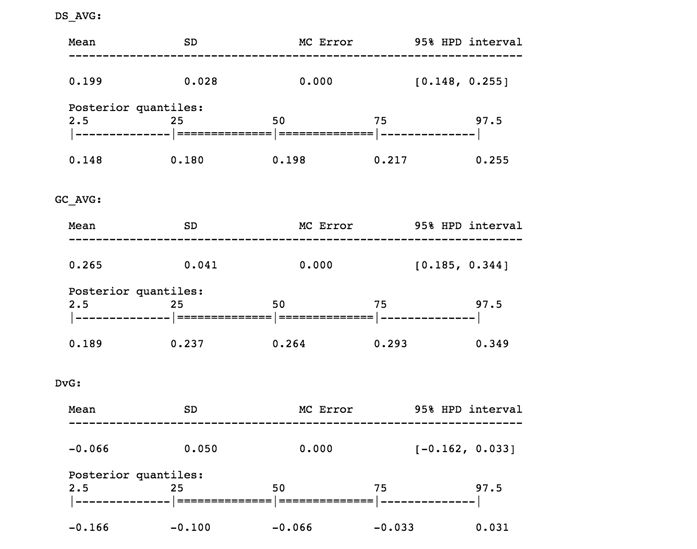
我們可以看到，對於DS和GC兩名選手，HPD區間和分位數區間要麽完全相同，要麽僅在小數點後略有不同。

問題是，我想根據AVG來判斷誰是更好的球員，目前看來，我還不能確定。至少我有95%的把握判定這兩名球員的AVG相差無幾。

計算的結果及生成的圖形顯示出這兩名球員AVG的差異在-0.162到0.033之間（我們用DvG（DS-GC）表示他們AVG的差異，如果DvG為正表示DS更好，反之則GC更好）。

從結果來看區間包括了0.000，這代表兩名球員的AVG不存在差異。因此，即使有證據表明GC比DS更優秀（因為DvG的後驗分布在負值區域的面積比在正值區域的面積更大），但是我有95%的把握判定這兩名球員的AVG並無差異。

也許有了更多的數據後，我可以確定他們之間的差異。畢竟，這就是貝葉斯理論的精髓所在。並不是說真相不存在，而是了解真相的過程很緩慢，隨著技術的不斷進步，我們能做的就是不斷修正我們的認知。

Python代碼和貝葉斯理論告訴你，誰是最好的棒球選手