原文地址：https://blog.csdn.net/qq_33913037/article/details/71328099

假如你是一個媒人，有若幹個單身男子登門求助，還有同樣多的單身女子也前來征婚。如果你已經知道這些女孩在每個男人心目中的排名，以及男孩們在每個女孩心中的排名(1)，你應該怎樣為他們牽線配對呢？
最好的配對方案當然是，每個人的另一半正好都是自己的“第一選擇”。這雖然很完美，但絕大多數情況下都不可能實現。比方說，男 1 號的最愛是女 1 號，而女 1 號的最愛不是男 1 號，這兩個人的最佳選擇就不可能被同時滿足。如果出現了好幾個男人的最愛都是同一個女孩兒的情況，這幾個男人的首選也不會同時得到滿足。當這種最為理想的配對方案無法實現時，怎樣的配對方案才能令人滿意呢？
其實，找的對象太完美不見得是個好事兒，和諧才是婚姻的關鍵。如果男 1 號和女 1 號各自有各自的對象，但男 1 號覺得，比起自己現在的對象，女 1 號更好一些；女 1 號也發現，在自己心目中，男 1 號的排名比現男友更靠前一些。這樣一來，這兩人就可能會發生外遇，最後扔下各自現在的對象，一起私奔了——因為這個結果對他們兩人都更好一些。在一種男女配對的方案中，如果出現了這種情況，我們就說婚姻搭配是不穩定的。作為一個紅娘，你深深地知道，對象介紹得不好沒有關系，就怕婚姻關系不穩定。給客戶牽線配對時，雖然不能讓每個人都得到最合適的，但婚姻搭配必須得是穩定的。換句話說，對於每一個人，在他心目中比他當前的伴侶更好的異性，都不會認為他也是一個更好的選擇。現在，我們的問題就是：穩定的婚姻搭配總是存在嗎？應該怎樣尋找出一個穩定的婚姻搭配？

為了便於分析，我們下面做一些約定。我們用字母 A 、 B 、 C 對男性進行編號，用數字 1 、 2 、 3 對女性進行編號。我們把所有男性從上到下列在左側，括號裏的數字表示每個人心目中對所有女性的排名；再把所有女性列在右側，用括號裏的字母表示她們對男性的偏好。圖 0-1 所示的就是有 2 男 2 女的一種情形，每個男的都更喜歡女 1 號，但女 1 號更喜歡男 B ，女 2 號更喜歡男 A 。若按 A-1 、 B-2 進行搭配，則男 B 和女 1 都更喜歡對方一些，這樣的婚姻搭配就是不穩定的。但若換一種搭配方案（如圖 0-2 ），這樣的搭配就是穩定的了。

圖 0-1 一個不穩定的婚姻搭配 男 B 和女 1 都不滿意現任伴侶

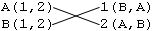
圖 0-2 一個穩定的婚姻搭配

可能很多人會立即想到一種尋找穩定婚姻搭配的策略：不斷修補當前搭配方案。如果兩個人互相之間都覺得對方比自己當前的伴侶更好，就讓這兩個人成為一對，剩下被甩的那兩個人組成一對。如果還有想要私奔的男女對，就繼續按照他們的願望對換情侶，直到最終消除所有的不穩定組合。容易看出，應用這種“修補策略”所得到的最終結果一定滿足婚姻的穩定性，但這種策略的問題就在於，它不一定有一個“最終結果”。事實上，按照上述方法反復調整搭配方案，最終有可能會陷入一個死循環，因此該策略甚至不能保證得出一個確定的方案來。

圖 0-3 應用“修補策略”可能會產生死循環

1962 年，美國數學家 David Gale 和 Lloyd Shapley 發明了一種尋找穩定婚姻的策略。不管男女各有多少人，不管他們各自的偏好如何，應用這種策略後總能得到一個穩定的婚姻搭配。換句話說，他們證明了穩定的婚姻搭配總是存在的。有趣的是，這種策略反映了現實生活中的很多真實情況。 在這種策略中，男人將一輪一輪地去追求他中意的女子，女子可以選擇接受或者拒絕她的追求者。第一輪，每個男人都選擇自己名單上排在首位的女人，並向她表白。此時，一個女孩兒可能面對的情況有三種：沒有人跟她表白，只有一個人跟她表白，有不止一個人跟她表白。在第一種情況下，這個女孩兒什麽都不用做，只需要繼續等待；在第二種情況下，接受那個人的表白，答應暫時和他做男女朋友；在第三種情況下，從所有追求者中選擇自己最中意的那一位，答應和他暫時做男女朋友，並拒絕其他所有的追求者。 第一輪結束後，有些男人已經有女朋友了，有些男人仍然是單身。在第二輪追女行動中，每個單身男都從所有還沒拒絕過他的女孩中選出自己最中意的那一個，並向她表白，不管她現在是否是單身。和第一輪一樣，女孩兒們需要從表白者中選擇最中意的一位，拒絕其他追求者。註意，如果這個女孩兒已經有男朋友了，當她遇到了更好的追求者時，她必須拒絕掉現在的男友，投向新的追求者的懷抱。這樣，一些單身男人將會得到女友，那些已經有了女友的人也可能會被甩掉，重新變成光棍。在以後的每一輪中，單身的男人繼續追求列表中的下一個女孩兒，女孩兒則從包括現男友在內的所有追求者中選擇最好的一個，並對其他人說不。這樣一輪一輪地進行下去，直到某個時候所有人都不再單身，下一輪將不會有任何新的表白發生，整個過程自動結束。此時的婚姻搭配就一定是穩定的了。

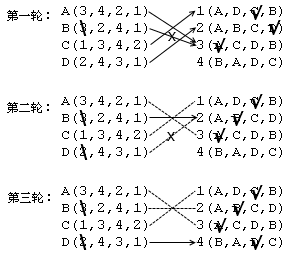
圖 0-4 應用上述策略，三輪之後將得出穩定的婚姻搭配

代碼是lrj大白書上的

#include <iostream>
#include <cstdio>
#include <sstream>
#include <cstring>
#include <map>
#include <set>
#include <vector>
#include <stack>
#include <queue>
#include <algorithm>
#include <cmath>
#define rap(i, a, n) for(int i=a; i<=n; i++)
#define MOD 2018
#define LL long long
#define ULL unsigned long long
#define Pair pair<int, int>
#define mem(a, b) memset(a, b, sizeof(a))
#define _  ios_base::sync_with_stdio(0),cin.tie(0)
//freopen("1.txt", "r", stdin);
using namespace std;
const int maxn = 1010, INF = 0x7fffffff;
int pref[maxn][maxn], order[maxn][maxn], next1[maxn];
int future_husband[maxn], future_wife[maxn];
queue<int> q;  //未訂婚男士隊列

//訂婚
void engage(int man, int woman)
{
    int m = future_husband[woman];
    if(m)                           //女士有現任未婚夫m
    {
        future_wife[m] = 0;         //拋棄m
        q.push(m);                  //m加入未訂婚男士隊列
    }
    future_wife[man] = woman;
    future_husband[woman] = man;
}

int main()
{
    int T;
    scanf("%d", &T);
    while(T--)
    {
        int n;
        scanf("%d", &n);
        for(int i=1; i<=n; i++)
        {
            for(int j=1; j<=n; j++)
                scanf("%d", &pref[i][j]);  //編號為i的男士第j個喜歡的人
            next1[i] = 1;                   //接下來應向排名為1的女士求婚
            future_wife[i] = 0;            //沒有未婚妻
            q.push(i);
        }

        for(int i=1; i<=n; i++)
        {
            for(int j=1; j<=n; j++)
            {
                int x;
                scanf("%d", &x);
                order[i][x] = j;           //編號為i的女士心目中，編號為x的男士的排名
            }
            future_husband[i] = 0;          //沒有未婚夫
        }
        while(!q.empty())
        {
            int man = q.front(); q.pop();
            int woman = pref[man][next1[man]++]; //下一個求婚對象
            if(!future_husband[woman])             //女士沒有未婚夫，直接訂婚
                engage(man, woman);
            else if(order[woman][man] < order[woman][future_husband[woman]])
                engage(man, woman);                 //代替女士現任的未婚夫
            else
                q.push(man);                        //直接被拒，下次再來
        }
        while(!q.empty()) q.pop();

        for(int i=1; i<=n; i++) printf("%d\n", future_wife[i]);
        if(T) printf("\n");
    }

    return 0;
}

穩定婚姻模型