https://www.luogu.org/problemnew/show/P2403

題目描述

在寬廣的非洲荒漠中，生活著一群勤勞勇敢的羊駝家族。被族人恭稱為“先知”的Alpaca L. Sotomon是這個家族的領袖，外人也稱其為“所駝門王”。所駝門王畢生致力於維護家族的安定與和諧，他曾親自率軍粉碎河蟹帝國主義的野蠻侵略，為族人立下赫赫戰功。所駝門王一生財寶無數，但因其生性節儉低調，他將財寶埋藏在自己設計的地下宮殿裏，這也是今天Henry Curtis故事的起點。Henry是一個愛財如命的貪婪家夥，而又非常聰明，他費盡心機謀劃了這次盜竊行動，破解重重機關後來到這座地下宮殿前。

整座宮殿呈矩陣狀，由R×C間矩形宮室組成，其中有N間宮室裏埋藏著寶藏，稱作藏寶宮室。宮殿裏外、相鄰宮室間都由堅硬的實體墻阻隔，由一間宮室到達另一間只能通過所駝門王獨創的移動方式——傳送門。所駝門王為這N間藏寶宮室每間都架設了一扇傳送門，沒有寶藏的宮室不設傳送門，所有的宮室傳送門分為三種：

1. “橫天門”：由該門可以傳送到同行的任一宮室；

2. “縱寰門”：由該門可以傳送到同列的任一宮室；

3. “自由*”：由該門可以傳送到以該門所在宮室為中心周圍8格中任一宮室（如果目標宮室存在的話）。

深謀遠慮的Henry當然事先就搞到了所駝門王當年的宮殿招標冊，書冊上詳細記錄了每扇傳送門所屬宮室及類型。而且，雖然宮殿內外相隔，但他自行準備了一種便攜式傳送門，可將自己傳送到殿內任意一間宮室開始尋寶，並在任意一間宮室結束後傳送出宮。整座宮殿只許進出一次，且便攜門無法進行宮室之間的傳送。不過好在宮室內傳送門的使用沒有次數限制，每間宮室也可以多次出入。

現在Henry已經打開了便攜門，即將選擇一間宮室進入。為得到盡多寶藏，他希望安排一條路線，使走過的不同藏寶宮室盡可能多。請你告訴Henry這條路線最多行經不同藏寶宮室的數目。

輸入輸出格式

輸入格式：

輸入文件sotomon.in第一行給出三個正整數N, R, C。

以下N行，每行給出一扇傳送門的信息，包含三個正整數xi, yi, Ti，表示該傳送門設在位於第xi行第yi列的藏寶宮室，類型為Ti。Ti是一個1~3間的整數，1表示可以傳送到第xi行任意一列的“橫天門”，2表示可以傳送到任意一行第yi列的“縱寰門”，3表示可以傳送到周圍8格宮室的“自由*”。

保證1≤xi≤R，1≤yi≤C，所有的傳送門位置互不相同。

輸出格式：

輸出文件sotomon.out只有一個正整數，表示你確定的路線所經過不同藏寶宮室的最大數目。

輸入輸出樣例

10 7 7
2 2 1
2 4 2
1 7 2
2 7 3
4 2 2
4 4 1
6 7 3
7 7 1
7 5 2
5 2 1

9

說明

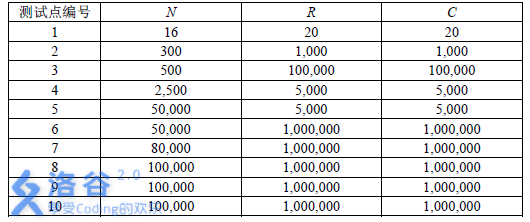
數據規模和約定：

1.首先需要動態開節點，然後通過門的類別建立節點之間的邊。

第一種：歸屬於x坐標對應的超級點，y坐標對應的點連向x坐標對應的點。

第二種：歸屬於y坐標對應的超級點，x坐標對應的點連向y坐標對應的點。

第三種：歸屬於本身（另開一個超級節點），搜索其周圍八個位置，若有節點，則由該店連接其對應的超級點。

2.對於第三種點的連邊，可以用hash優化，也可以用map。

3.最後就是縮點，跑拓撲圖了。

  1 #include<bits/stdc++.h>
  2 #define ll long long
  3 using namespace std;
  4 int n,a,b,col[3000050],now;
  5 int dfn[3000050],low[3000050],cnt,sum;
  6 int t[3000050],du[3000050],top;
  7 int dis[300050],ans;
  8 int posx[1000050],posy[1000050],tot;
  9 struct nde
 10 {
 11     int siz[3000050],head[3000050],nex[8000050],ver[8000050],tot;
 12     void add(int x,int y)
 13     {
 14         nex[++tot]=head[x];
 15         ver[tot]=y;
 16         head[x]=tot;
 17     }
 18 }tp1,tp2;
 19 struct noe
 20 {
 21     #define p 1112017
 22     int head[1200050],nex[1000050],pos[1000050],tot;
 23     ll val[1000050];
 24     void add(int x,int y,int f)
 25     {
 26         ll v=(ll)b*x+y;
 27         val[++tot]=v;
 28         nex[tot]=head[v%p];
 29         head[v%p]=tot;
 30         pos[tot]=f;
 31     }
 32     int find(int x,int y)
 33     {
 34         if(x<1||x>a||y<1||y>b)
 35             return 0;
 36         ll v=(ll)b*x+y;
 37         for(int i=head[v%p];i;i=nex[i])
 38             if(val[i]==v)
 39                 return pos[i];
 40         return 0;
 41     }
 42     #undef p
 43 }hash;
 44 struct node
 45 {
 46     int x,y,flag,pos;
 47 }num[1000050];
 48 void tarjan(int u)
 49 {
 50     dfn[u]=low[u]=++cnt;
 51     t[++top]=u;
 52     for(int i=tp1.head[u];i;i=tp1.nex[i])
 53         if(!dfn[tp1.ver[i]])
 54         {
 55             tarjan(tp1.ver[i]);
 56             low[u]=min(low[u],low[tp1.ver[i]]);
 57         }
 58         else if(!col[tp1.ver[i]])
 59             low[u]=min(low[u],dfn[tp1.ver[i]]);
 60     if(low[u]==dfn[u])
 61     {
 62         ++sum;
 63         while(t[top+1]!=u)
 64         {
 65             tp2.siz[sum]+=tp1.siz[t[top]];
 66             col[t[top--]]=sum;
 67         }
 68     }
 69 }
 70 void spfa()
 71 {
 72     queue<int > q;
 73     for(int i=1;i<=sum;++i)
 74         if(!du[i])
 75         {
 76             q.push(i);
 77             dis[i]=tp2.siz[i];
 78         }
 79     while(!q.empty())
 80     {
 81         int u=q.front();q.pop();
 82         ans=max(ans,dis[u]);
 83         for(int i=tp2.head[u];i;i=tp2.nex[i])
 84         {
 85             int v=tp2.ver[i];
 86             dis[v]=max(dis[v],dis[u]+tp2.siz[v]);
 87             if(!--du[v])
 88                 q.push(v);
 89         }
 90     }
 91 }
 92 int main()
 93 {
 94     scanf("%d%d%d",&n,&a,&b);
 95     for(int i=1;i<=n;++i)
 96     {
 97         scanf("%d%d%d",&num[i].x,&num[i].y,&num[i].flag);
 98         if(num[i].flag==1)
 99             num[i].pos=(posx[num[i].x]? posx[num[i].x]:posx[num[i].x]=++tot);
100         else if(num[i].flag==2)
101             num[i].pos=(posy[num[i].y]? posy[num[i].y]:posy[num[i].y]=++tot);
102         else
103             num[i].pos=++tot;
104         ++tp1.siz[num[i].pos];
105         hash.add(num[i].x,num[i].y,num[i].pos);
106     }
107     for(int i=1;i<=n;++i)
108         if(num[i].flag==1)
109         {
110             if(posy[num[i].y])
111             tp1.add(posy[num[i].y],posx[num[i].x]);
112         }
113         else if(num[i].flag==2)
114         {
115             if(posx[num[i].x])
116             tp1.add(posx[num[i].x],posy[num[i].y]);
117         }
118         else
119         {
120             if(posx[num[i].x])
121                 tp1.add(posx[num[i].x],num[i].pos);
122             if(posy[num[i].y])
123                 tp1.add(posy[num[i].y],num[i].pos);
124             for(int x=-1;x<=1;++x)
125                 for(int y=-1;y<=1;++y)
126                     if(tp1.siz[now=hash.find(num[i].x+x,num[i].y+y)])
127                         tp1.add(num[i].pos,now);
128         }
129     for(int i=1;i<=tot;++i)
130         if(!dfn[i])
131             tarjan(i);
132     for(int i=1;i<=tot;++i)
133         for(int j=tp1.head[i];j;j=tp1.nex[j])
134             if(col[i]!=col[tp1.ver[j]])
135             {
136                 ++du[col[tp1.ver[j]]];
137                 tp2.add(col[i],col[tp1.ver[j]]);
138             }
139     spfa();printf("%d",ans);
140     return 0;
141 }

P2403 [SDOI2010]所駝門王的寶藏