馬氏距離的深入理解
轉自：https://www.cnblogs.com/likai198981/p/3167928.html
對於馬氏距離，本人研究了一下，雖然看上去公式很簡單的，但是其中存在很多模糊的東西，例如有很多教科書以及網路上的簡要說明，下面以維基百科作為引用：
馬氏距離是由印度統計學家馬哈拉諾比斯（P. C. Mahalanobis）提出的，表示資料的協方差距離。它是一種有效的計算兩個未知樣本集的相似度的方法。與歐氏距離不同的是它考慮到各種特性之間的聯絡（例如：一條關於身高的資訊會帶來一條關於體重的資訊，因為兩者是有關聯的）並且是尺度無關的（scale-invariant），即獨立於測量尺度。 對於一個均值為
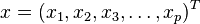，其馬氏距離為
馬氏距離也可以定義為兩個服從同一分佈並且其協方差矩陣為Σ的隨機變數
與
的差異程度：
如果協方差矩陣為單位矩陣，馬氏距離就簡化為歐式距離；如果協方差矩陣為對角陣，其也可稱為正規化的馬氏距離。
其中σi是xi的標準差。
對於上述的馬氏距離，本人研究了一下，雖然看上去公式很簡單的，但是其中存在很多模糊的東西，為什麼馬氏距離是一種考濾到各種特性之間的聯絡並且是尺度無關的？為什麼可以使用協方差矩陣的逆矩陣去掉單位而使之尺度無關。基於此，以下是個人的一些想法。
1、為什麼要使變數去掉單位而使尺度無關
基於歐氏距離，兩個點之間的長度為：
每個變數之間的變數之間的尺度都不一樣，例如第一個變數的數量級是1000,而第二個變數是變數的數量級是10，如v1=(3000,20),v2 = (5000,50),那麼如果只有2維的點中，歐氏距離為：
由上面可以很容易看出，當兩個變數都變成數量級為10的時候，第一個變數存在一個權重：10，因而如果不使用相同尺度的時候，不同尺度的變數就會在計算的過程中自動地生成相應的權重。因而，如果兩個變數在現實中的權重是相同的話，就必須要先化成相同的尺度，以減去由尺度造成的誤差，這就是標準化的由來。
如果化成相同尺度的方法就變成標準化方法了，標準化的方法有很多種，有些辦法是使資料化成[0,1]之間，如min-max標準化，有些通過原始資料減去平均值再除標準差的方法，如z-score標準化，有些類似如上面的方法那樣，化成相同的數量級的方法，如decimal scaling小數定標標準化。
2、為什麼馬氏距離是與尺度無關的？
根據上面1所描述，當計算兩點的相似度（也可以說是距離的時候），第一步是首先標準化，化成與尺度無關的量，再計算它的距離。但是如果是單純使每個變數先標準化，然後再計算距離，可能會出現某種錯誤，原因是可能在有些多維空間中，某個兩個維之間可能是線性相關的，如下圖所示(引用自：http://xgli0910.blog.163.com/blog/static/46962168201021932741868/）：
黃色部分為樣品點，可以知道x1與x2是線性相關的，根據正態分佈，對於中心點u，與A與B的標準距離應該是相同的，而馬氏距離能做到這一點，但歐氏距離做不到，如下圖所示：
由上圖看到，如果使用歐氏距離，A點與B點距離中心點相同，但是又可以看出，A點處於樣品集的邊緣了，再外出一點就成異常點了。因此我們使用歐氏距離計算的時候，不能有效地區分出異常資料，看不出兩變數之間的相似性與差異性，而上圖中，A與B對於全體樣品來說，差異性是夠大的了。
為了解決這個問題，我們可以通過旋轉座標軸的方法，如下圖所示：
可以看到y1與y2是線性無關的，因此我們可以通過對線性無關的分量進行標準化後，再求得距離是合理的。其實通過旋轉座標軸的方式，相當於對x進行相應的線性變換：Y = PX,使Y裡面的各分變數變成線性無關的。設 是隨機向量
=[x1,x2,...xp]的協方差矩陣，它有特徵值-特徵向量對(λ1,e1)， (λ2,e2)，.....(λp,ep)，其中λ1>=λ2>=....>=λp，則第i主成分由
因此得到的新的變數Y裡面的各分量是線性無關的，此時對於離中心點距離為某常數C形成的曲面是超橢球面。而yi的方差為λi，因而需要再把yi標準化，使之變成yi/λi，形成新的yi,這樣生成的yi之間變成了與尺度無關的變量了，公式如下：
其中P是以特徵向量為行向量的矩陣，根據正定距陣，特徵向量互相正交。
現在來驗證Y的協方差：
所以，對於旋轉壓縮後的Y的各分量之間線無關，而且已經標準化，與尺度無關，此時以Y分量為座標軸形成的空間中，離中心距離為常數C的面為正圓球面。因而可以直接使用歐氏距離描述兩點之間的相似度，也就是距離，因此有：
因此，當原座標經過適當的變換之後，可以求出兩點與尺度無關的距離，這也是使用馬氏距離的原因。
參考書籍：實用多元統計分析-第六版，Rechard A.Johnson （關於距離、主成分分析）