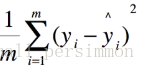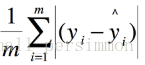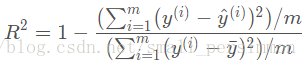演算法學習——線性迴歸
1.線性迴歸模型表示
一元線性迴歸表示:
多元線性迴歸表示:
矩陣表示:,其中
2.目標函式——平方損失函式
一個數據點為的誤差:
誤差損失總和——殘差:
使用殘差的平方和(RSS)或最小化均方誤差(MSE)來表示所有樣本點的誤差「平方損失函式」:
3.最小二乘的概率解釋
4.最小二乘解法一——梯度下降
梯度下降是一個需要進行迭代的,求區域性最小值的演算法,下面給出迭代規則:
把帶入並求
的偏導數即可得到更新規則,:= 在這裡表示賦值,當只有一個樣本的時候,更新規則如下:
帶入(11),得到:
每做一次求導都表示找到了當前位置梯度最陡的方向,代表學習速率,即步長。
下面提供三種具體的實施方式:
- 批量梯度下降(BGD)
批梯度下降一次迭代會更新所有θ,每次更新都是向著最陡的方向前進。每一次迭代都需要把所有的樣本(共m個)取到,把每一個樣本的真實值減去預測值,再把這個差值乘上該樣本的第i個特徵。重複迭代p次之後收斂了(當兩次迭代的值幾乎不發生變化時,可判斷收斂),然後又重複如上步驟獲得θ1、θ2、……θn,最後取得最終的引數向量θ,去畫出我們的預測直線。
優點:得到全域性最優解,易於並行實現
缺點:當樣本數目很多時,訓練過程會很慢
- 隨機梯度下降(SGD)
隨機梯度下降法為最小化每條樣本的損失函式,雖然不是每次迭代得到的損失函式都向著全域性最優方向, 但是大的整體的方向是向全域性最優解的,最終的結果往往是在全域性最優解附近。 也就是說我用樣本中的一個例子來近似我所有的樣本,來調整θ,其不會計算斜率最大的方向,而是每次只選擇一個維度踏出一步;下降一次迭代只更新某個θ,抱著並不嚴謹的走走看的態度前進。
優點:訓練速度快
缺點:準確度下降,並不是全域性最優,不易與並行實現
- 小批量梯度下降(MBGD)
MBGD是一種介於SGD和BGD兩種方法之間的一種折中的梯度下降法:在每一步中,不是基於完整訓練集(如BGD)或僅基於一個例項(如SGD中那樣)計算梯度,而是在小隨機例項集上的梯度。
5.最小二乘解法二——正規方程組
可以通過直接求出最小值點,在最小值點,
各個方向的偏導均為零。
6.評價指標
均方誤差(MSE)
均方根誤差(RMSE)
平均絕對誤差(MAE)
R-Squared
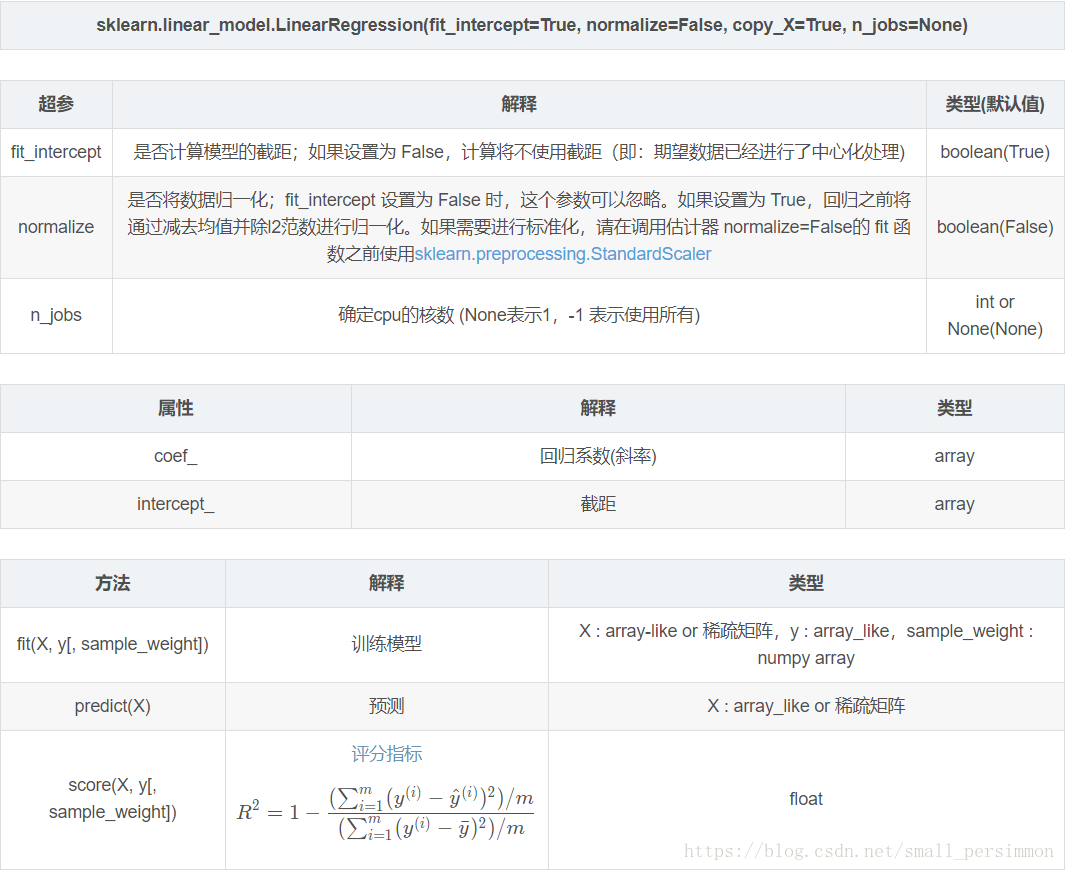
7.演算法實現
引數解釋:
調包實踐:
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_score
experiences = np.array([0,1,2,3,4,5,6,7,8,9,10])
salaries = np.array([103100, 104900, 106800, 108700, 110400, 112300, 114200, 116100, 117800, 119700, 121600])
# 將特徵資料集分為訓練集和測試集,除了最後5個作為測試用例,其他都用於訓練
X_train = experiences[:7]
X_train = X_train.reshape(-1,1)
X_test = experiences[7:]
X_test = X_test.reshape(-1,1)
# 把目標資料(特徵對應的真實值)也分為訓練集和測試集
y_train = salaries[:7]
y_test = salaries[7:]
# 建立線性迴歸模型
regr = linear_model.LinearRegression()
# 用訓練集訓練模型——看就這麼簡單,一行搞定訓練過程
regr.fit(X_train, y_train)
# 用訓練得出的模型進行預測
diabetes_y_pred = regr.predict(X_test)
# 將測試結果以圖示的方式顯示出來
plt.scatter(X_test, y_test, color='black')
plt.plot(X_test, diabetes_y_pred, color='blue', linewidth=3)
plt.xticks(())
plt.yticks(())
plt.show()
參考連結:
線性迴歸、邏輯迴歸、廣義線性模型——斯坦福CS229機器學習個人總結(一)