機器學習-線性迴歸
本文參考吳恩達機器學習課程第2章
線性迴歸公式:
f(x)=θ0+θ1x 代價公式(誤差均值中的2用來抵消求導得來的2): J(θ0,θ1)=2m1∑i=1m(fθ(x)i−yi)2
目標:代價最小化
這裡演示單變數線性迴歸時: 令θ0=0, f(x)=θ1x 可對J(θ1)求導, J′(θ1)=m1∑i=1m(θ1xi−yi) 此時J′(θ1)=0方可求出θ1
實際上,由於代價函式經常含有2個及以上引數,目前函式處於三維空間x, y, z分別為θ0,θ1,
梯度下降法
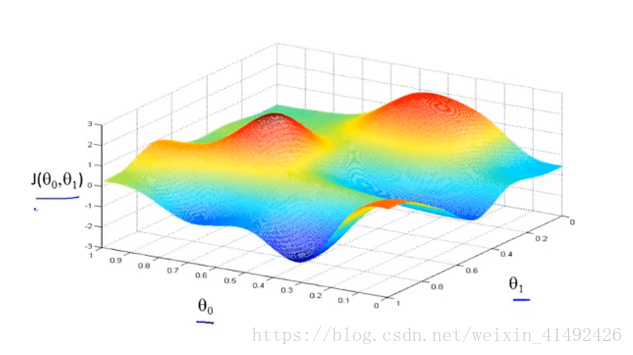
具體展開: θ0:=θ0−αdθ0dJ(θ0,θ1)=θ0−m1∑i=1m(θ0+θ1xi−yi) θ1:=θ1−αdθ1dJ(θ0,θ1)=θ0−m1∑i=1m(θ0+θ1xi−yi)∗xi
- 導數項: 達到區域性最優解時(圖中某一處區域性最低點時),此時導數項為0,θi:=θi−α∗0,引數不再更新,且隨著J(θ)接近最低點,導數項也會越來越小,所以暫時學習率可不變。
- 梯度下降可以用於更新任何可微(因為需要求導)的代價函式J,目前使用的梯度下降用到了∑i=1m,意味著每下降一次遍歷一整個資料集,也稱batch梯度下降演算法。
相關推薦
Windons10 python3.6 機器學習線性迴歸 matplotlib出現影象中文亂碼和使用sk_learn輸出ValueError: Expected 2D array, got 1D
Windons10 python3.6 機器學習線性迴歸 matplotlib出現影象中文亂碼和使用sk_learn輸出ValueError: Expected 2D array, got 1D array instead:問題解決 話不多說,大家來就是解決問題的,本人也是遇到問題才四處搜尋
機器學習-線性迴歸(LMS Algorithm)
今天正式開始機器學習之路(看的斯坦福大學的視訊課以及講義),由於看的時候濛濛的,因此想要找個平臺儲存一下自己學習的成果,因此寫了此篇文章,作為機器學習的小白,文章可能有諸多不妥之處,不作為學術理論的深入研究範圍。因為我是小白,我是小白,我是小白。 由於第一次用簡書寫,所以可能格式不太對,請見諒。
機器學習 --- 線性迴歸與邏輯迴歸
線性迴歸和邏輯迴歸在機器學習上是一種監督式學習。在預測類問題上,我們希望能通過一個對映關係 ,當給定變數 ,能得到一個較為滿意的預測結果 ,迴歸方法旨在找到能表示樣本空間分佈的對映關係。 一、線性迴歸的基本形式
機器學習--線性迴歸演算法預測房價
裡面非常詳細地介紹了微積分基本運演算法則、線性迴歸演算法、梯度下降演算法及改進。 a. 用線性迴歸方法擬合正弦函式 %matplotlib inline import matplotlib.pyplot as plt import numpy as np # 生成2
機器學習——線性迴歸
1 def test_fj(): 2 X = np.array([[500, 3, 0.3], [1000, 1, 0.6], [750, 2, 0.3], [600, 5, 0.2], [1200, 1, 0.6]], dtype=float) 3 Y = np.array([100
機器學習-線性迴歸(LMS Algorithm)
今天正式開始機器學習之路(看的斯坦福大學的視訊課以及講義),由於看的時候濛濛的,因此想要找個平臺儲存一下自己學習的成果,因此寫了此篇文章,作為機器學習的小白,文章可能有諸多不妥之處,不作為學術理論的深入研究範圍。因為我是小白,我是小白,我是小白。 由於第一次用簡書寫,所以可
機器學習-線性迴歸
本文參考吳恩達機器學習課程第2章 線性迴歸公式: f(x)=θ0+θ1xf(x)=\theta_0 + \theta_1xf(x)=θ0+θ1x 代價公式(誤差均值中的2用來抵消求導得來的2): J(θ0,θ1)=12m∑i=1m(fθ(x)i−yi)2J(
機器學習--線性迴歸1(一元線性迴歸、多元線性迴歸,誤差性質)
前面幾節都是監督學習方面的演算法,監督學習是指有目標變數或預測目標的機器學習方法,迴歸與分類的不同,就在於其目標變數是連續數值型,而分類的目標變數是標稱型資料,其實前面的Logistic迴歸就是迴歸的一種,他們的處理方法大同小異,在這裡系統的講解一下回歸的來龍去脈,理解影響迴
機器學習----線性迴歸原理---最下二乘法和梯度下降怎麼來的-----專案預測大學生是否被錄取程式碼案例
這節課說明了 最下二乘法 是怎麼來的。 接下來是面試需要問的 誤差,(機器學習是建立在獨立同分布的基礎上,事實上,根本無法證明獨立同分布而且是正態分佈,我們假設的,只要模型可用,就可以) 獨立: 每個人的
機器學習|線性迴歸三大評價指標實現『MAE, MSE, MAPE』(Python語言描述)
對於迴歸預測結果,通常會有平均絕對誤差、平均絕對百分比誤差、均方誤差等多個指標進行評價。這裡,我們先介紹最常用的3個: 平均絕對誤差(MAE) 就是絕對誤差的平均值,它的計算公式如下: M
【Stanford|斯坦福-機器學習:線性迴歸-單特徵梯度下降+動態圖】python3實現
五、完整測試程式碼實現 # coding=utf-8 # 線性迴歸-單特徵梯度下降練習 from numpy import * import matplotlib.pyplot as plt from matplotlib import animation import numpy as np # 【1
機器學習 -- 線性迴歸和邏輯迴歸的區別
迴歸演算法是一種通過最小化預測值與實際結果值之間的差距,而得到輸入特徵之間的最佳組合方式的一類演算法。對於連續值預測有線性迴歸等,而對於離散值/類別預測,我們也可以把邏輯迴歸等也視作迴歸演算法的一種。 線性迴歸與邏輯迴歸是機器學習中比較基礎又很常用的內容。線性迴歸主
機器學習 線性迴歸 (matlab實現)
代價函式:下降梯度:假設函式:x代表年齡,y代表身高預測身高與年齡的關係Code:x = load('ex2x.dat'); y = load('ex2y.dat'); [m,n] = size(x); x = [ones(m,1),x];%偏置項 x0 = 1 figur
機器學習--線性迴歸R語言
迴歸分析就是利用樣本,產生擬合方程,從而進行預測。簡而言之,就是你用你手頭上的資料進行模型的訓練,然後用你得到的模型對於新資料進行預測。 一元線性迴歸: 例子: y<- c(61,57,58,40,90,35,68)#weight x&l
機器學習線性迴歸中,用矩陣求導方法求最小二乘法的方法
在我們推導最小二乘法的時候,Andrew提供了兩種方法,一個是梯度下降法則,另一個是矩陣求導法則。後來在《機器學習實戰裡》面看線性迴歸程式碼的時候,裡面就是用了矩陣求導法則。要看懂矩陣求導法則,是需要一些矩陣論的知識的,還記得今年夏天我在苦逼地到處求矩陣論地速成
機器學習--線性迴歸--梯度下降的實現
## 機器學習--線性單元迴歸--單變數梯度下降的實現 ### 【線性迴歸】 ```text 如果要用一句話來解釋線性迴歸是什麼的話,那麼我的理解是這樣子的: **線性迴歸,是從大量的資料中找出最優的線性(y=ax+b)擬合函式,通過資料確定函式中的未知引數,進而進行後續操作(預測) **迴歸的概念是從統
圖解機器學習-監督學習-線性迴歸總結
code:1.分析資料需要用什麼函式來擬合,給定已知sin函式的時候好擬合,但是未知函式是幾次,未知具體函式什麼樣子的時候擬合的時候需要自己觀察資料,並選擇相應的模型擬合,我自己編寫了一段code,擬合一下試試演算法的實用性. x=[1,3,5,6,2,4]'; y=[3,4,5,6,7,
機器學習之迴歸(1)線性迴歸
# -*- coding: utf-8 -*- """ Created on Sun Apr 15 16:18:34 2018 @author: Administrator """ import matplotlib.pyplot as plt #pyplo
機器學習->監督學習->線性迴歸(LASSO,Ridge,SGD)
本篇博文主要總結線性迴歸,線性迴歸雖然簡單,但是卻是很重要,我將沿著以下幾個主題總結 最小二乘法 使用極大似然估計來解釋最小二乘 的解析式的求解過程 線性迴歸的複雜度懲罰因子(LASSO,Ridge) 梯度下降法 實戰 最小二乘法 線性迴歸,線性是
機器學習--線性單元迴歸--單變數梯度下降的實現
## 機器學習--線性單元迴歸--單變數梯度下降的實現 ### 【線性迴歸】 ```text 如果要用一句話來解釋線性迴歸是什麼的話,那麼我的理解是這樣子的: **線性迴歸,是從大量的資料中找出最優的線性(y=ax+b)擬合函式,通過資料確定函式中的未知引數,進而進行後續操作(預測) **迴歸的概念是從統
