向量點乘與向量叉乘的意義
阿新 • • 發佈:2018-11-04
今天學習OpenGL的時候,看到教程上面光照部分關於向量乘積之間的的程式碼,由於之前沒有好好學習數學,所以感到十分的懵逼,在網上看了一個部落格之後感到豁然開朗。這是部落格原文:向量點乘與叉乘的幾何意義。我主要是為了方便自已以後新增和查詢。
向量的點積公式為:a * b = |a| * |b| * cosθ,點積的結果是數量而不是向量所以點積也被稱為數量積或者內積,是a向量在b向量上投影的長度與b向量的長度的乘積,是標量,反映了兩個向量之間的相似度,兩向量越相似,它們的點積就越大。
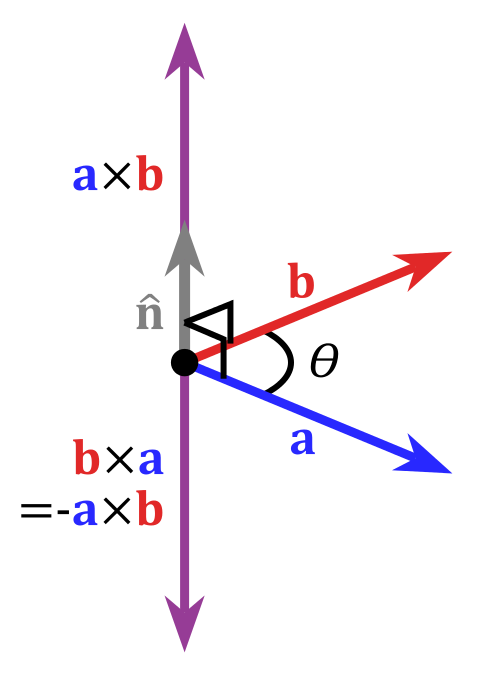
向量的叉乘公式為:a ^ b = |a| * |b| * sinθ,叉乘的結果是一個新的向量,所以也稱為向量積,它垂直於相乘的a、b兩向量所構成的平面。
向量積被定義為:
模長:(在這裡θ表示兩向量之間的夾角(共起點的前提下)(0° ≤ θ ≤ 180°),它位於這兩個向量所定義的平面上。)
方向:a向量與b向量的向量積的方向與這兩個向量所在平面垂直,且遵守右手定則。(一個簡單的確定滿足“右手定則”的結果向量的方向的方法是這樣的:若座標系是滿足右手定則的,當右手的四指從a以不超過180度的轉角轉向b時,豎起的大拇指指向是c的方向。c = a ∧ b)
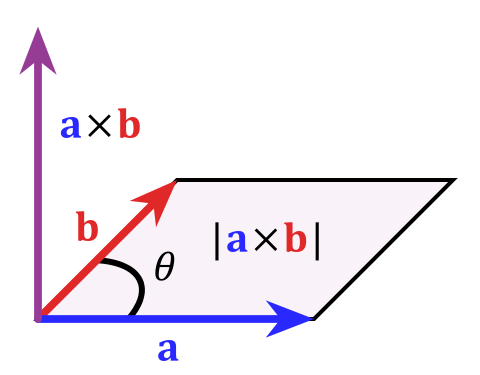
特別的,在二維中,兩個向量的向量積的模的絕對值等於由這兩天向量組成的平行四邊形的面積。