a/b（當b不為0的時候有意義）；同理你理解逆矩陣就是與矩陣成導數關係。

那麼行列式的值不為0，就說明逆矩陣存在，這樣就合情合理了。

首先，我們先來看看這個數的倒數：

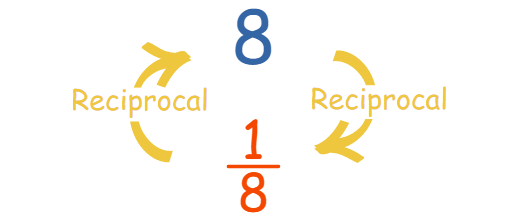
·倒數

其實矩陣的逆矩陣也跟倒數的性質一樣，不過只是我們習慣用A-1表示：

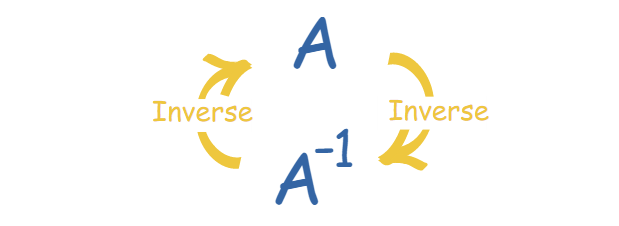
問題來了，既然是和倒數的性質類似，那為什麼不能寫成1/A？

其實原因很簡單，主要是因為矩陣不能被除。不過 1/8倒可以被寫成 8-1。

那矩陣的逆和倒數還有其他相似之處嗎？

• 當我們將一個數乘以它的倒數我們得到1。

8 × (1/8) = 1

• 當一個矩陣乘以逆時，我們得到了單位矩陣（而單位矩陣，其實也就是矩陣中的“1”）。

A × A-1 = I

• 而此時我們將矩陣的逆放在前面，很明顯，結果還是一樣的

(1/8) × 8 = 1

A-1 × A = I

模友：超模君，剛才講的“單位矩陣”是什麼意思，你還沒說明呢

超模君：別急，慢慢來！關於單位矩陣，其實就是一個相當於數字“1”的矩陣：

·3x3的單位矩陣

那怎樣的矩陣才是單位矩陣呢？

①它是“正方形”（行數與列數相同）；

②它的對角線上的數字都是1，其他地方都是0。

• 那問題來了，我們該如何去計算矩陣的逆呢？

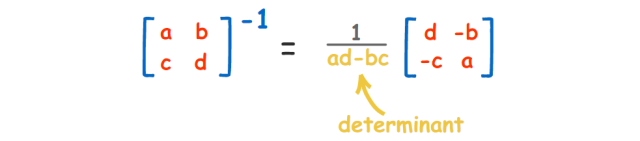
換句話說：交換a和d的位置，將負數置於b和c的前面，並將所有事物除以行列式（ad-bc）

舉個栗子：

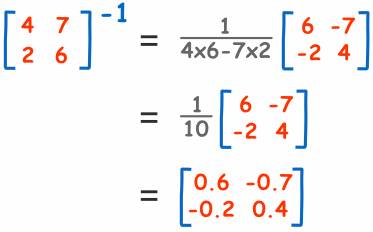
不過該如何去判斷這是正確的答案呢？

那這個時候就要用到我們最開始講的公式：

A × A-1 = I

所以，讓我們檢查一下，當我們將矩陣乘以矩陣的逆時，會是怎樣的？

嘿嘿嘿嘿！我們最終得到了單位矩陣！

留個作業：試試這樣，能不能得到單位矩陣呢？

其實，在瞭解矩陣的過程中，總是會有個疑問：為什麼我們需要矩陣的逆呢？

其主要原因是：矩陣沒辦法被除。（這個時間各位模友可以回想一下：是不是從來都沒看過矩陣被除）

換句話說，矩陣根本就沒有被除的概念

。

而矩陣的逆，正好是被我們用來解決“矩陣除法”的問題。