題目描述

有 $n$ 個同學（編號為 $1$ 到 $n$ ）正在玩一個資訊傳遞的遊戲。在遊戲裡每人都有一個固定的資訊傳遞物件，其中，編號為 $i$ 的同學的資訊傳遞物件是編號為 TiT_iTi​ 的同學。

遊戲開始時，每人都只知道自己的生日。之後每一輪中，所有人會同時將自己當前所知的生日資訊告訴各自的資訊傳遞物件（注意：可能有人可以從若干人那裡獲取資訊， 但是每人只會把資訊告訴一個人，即自己的資訊傳遞物件）。當有人從別人口中得知自 己的生日時，遊戲結束。請問該遊戲一共可以進行幾輪？

輸入輸出格式

輸入共2行。 第1行包含1個正整數 $n$ ，表示 $n$ 個人。

第2行包含 $n$ 個用空格隔開的正整數 T1,T2,⋯⋯,TnT_1,T_2,\cdots\cdots,T_nT1​,T2​,⋯⋯,Tn​ ，其中第 $i$ 個整數 TiT_iTi​ 表示編號為 $i$ 的同學的資訊傳遞物件是編號為 TiT_iTi​ 的同學， Ti≤nT_i \leq nTi​≤n 且 Ti≠iT_i \neq iTi​≠i 。

輸出共1行，包含1個整數，表示遊戲一共可以進行多少輪。

輸入輸出樣例

5
2 4 2 3 1

3

說明

樣例1解釋

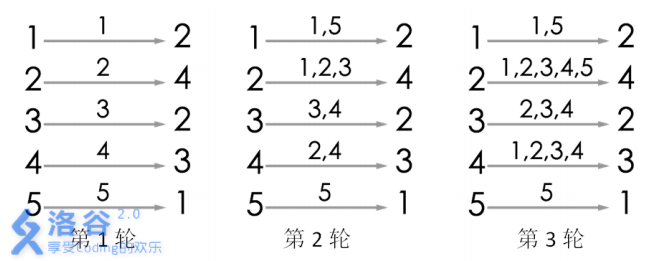
遊戲的流程如圖所示。當進行完第 3 輪遊戲後， 4 號玩家會聽到 2 號玩家告訴他自

己的生日，所以答案為 3。當然，第 3 輪遊戲後， 2 號玩家、 3 號玩家都能從自己的訊息

來源得知自己的生日，同樣符合遊戲結束的條件。

對於 30%的資料， n ≤ 200；

對於 60%的資料， n ≤ 2500；

對於 100%的資料， n ≤ 200000。

顯而易見，按照題目中給的樣例解釋我們是很難看懂的。

這道題在洛谷中的標籤是並查集和圖論。

但是我沒有用到並查集而是拓撲排序+建圖遍歷。

為什麼我會想到拓撲排序呢？

題目中給出每個同學只能把資訊交給一個其他的同學。

所以我們可以根據題意建立一個有向圖。

然後找到最小環，即為遊戲可以進行的輪數。

所以我們可以先用拓撲排序刪去不在環中的點。

然後遍歷一遍圖找到最小環直接輸出就行了。

#include<cstdio>
#include<iostream>
#include<cstring>
using namespace std;
const int MAXN=200000;
int t[MAXN],n,ans=19260817,dg[MAXN],tot=0;
bool flag=0,visit[MAXN];
void topsort()
{
	int q[MAXN*5];
	int head=1,tail=1;
	for(int i=1;i<=n;i++)
		if(!dg[i])
			q[++tail]=i;
	while(head<=tail)
	{
		int x=q[head++];
		int v=t[x];
		dg[v]--;
		if(!dg[v])
			q[++tail]=v;
	}
}
void dfs(int x,int step)
{
	if(!t[x])
		return ;
	if(flag)
		return ;
	if(visit[x])
	{
		ans=min(ans,step);
		flag=1;
		return ;
	}
	visit[x]=1;
	dfs(t[x],step+1);
}
int main()
{
	int x;
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		cin>>x;
		dg[x]++;
		t[i]=x;
	}
	topsort();
	for(int i=1;i<=n;i++)
	{
		if(dg[i]>0&&visit[i]==0)
		{flag=0; dfs(i,0);}
	}
	cout<<ans;
	return 0;
}