反向傳導(BP)演算法
假設我們有一個固定樣本集 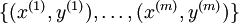 ,它包含
,它包含 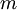 個樣例。我們可以用批量梯度下降法來求解神經網路。具體來講,對於單個樣例
個樣例。我們可以用批量梯度下降法來求解神經網路。具體來講,對於單個樣例 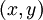 ,其代價函式為:
,其代價函式為:
這是一個(二分之一的)方差代價函式。給定一個包含 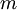 個樣例的資料集,我們可以定義整體代價函式為:
個樣例的資料集,我們可以定義整體代價函式為:
以上關於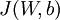 定義中的第一項是一個均方差項。第二項是一個規則化項(也叫權重衰減項),其目的是減小權重的幅度,防止過度擬合。
定義中的第一項是一個均方差項。第二項是一個規則化項(也叫權重衰減項),其目的是減小權重的幅度,防止過度擬合。
[注:通常權重衰減的計算並不使用偏置項 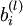 ,比如我們在
,比如我們在 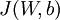 的定義中就沒有使用。一般來說,將偏置項包含在權重衰減項中只會對最終的神經網路產生很小的影響。如果你在斯坦福選修過CS229(機器學習)課程,或者在YouTube上看過課程視訊,你會發現這個權重衰減實際上是課上提到的貝葉斯規則化方法的變種。在貝葉斯規則化方法中,我們將高斯先驗概率引入到引數中計算MAP(極大後驗)估計(而不是極大似然估計)。]
的定義中就沒有使用。一般來說,將偏置項包含在權重衰減項中只會對最終的神經網路產生很小的影響。如果你在斯坦福選修過CS229(機器學習)課程,或者在YouTube上看過課程視訊,你會發現這個權重衰減實際上是課上提到的貝葉斯規則化方法的變種。在貝葉斯規則化方法中,我們將高斯先驗概率引入到引數中計算MAP(極大後驗)估計(而不是極大似然估計)。]
權重衰減引數 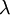 用於控制公式中兩項的相對重要性。在此重申一下這兩個複雜函式的含義:
用於控制公式中兩項的相對重要性。在此重申一下這兩個複雜函式的含義: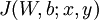 是針對單個樣例計算得到的方差代價函式;
是針對單個樣例計算得到的方差代價函式;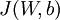 是整體樣本代價函式,它包含權重衰減項。
是整體樣本代價函式,它包含權重衰減項。
以上的代價函式經常被用於分類和迴歸問題。在分類問題中,我們用 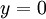 或
或 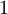 ,來代表兩種型別的標籤(回想一下,這是因為 sigmoid啟用函式的值域為
,來代表兩種型別的標籤(回想一下,這是因為 sigmoid啟用函式的值域為 ![\textstyle [0,1]](http://ufldl.stanford.edu/wiki/images/math/8/4/2/84235d31ac83fe764546463aba7acc0e.png) ;如果我們使用雙曲正切型啟用函式,那麼應該選用
;如果我們使用雙曲正切型啟用函式,那麼應該選用 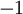 和
和 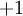 作為標籤)。對於迴歸問題,我們首先要變換輸出值域(譯者注:也就是
作為標籤)。對於迴歸問題,我們首先要變換輸出值域(譯者注:也就是  ),以保證其範圍為
),以保證其範圍為 ![\textstyle [0,1]](http://ufldl.stanford.edu/wiki/images/math/8/4/2/84235d31ac83fe764546463aba7acc0e.png) (同樣地,如果我們使用雙曲正切型啟用函式,要使輸出值域為
(同樣地,如果我們使用雙曲正切型啟用函式,要使輸出值域為 ![\textstyle [-1,1]](http://ufldl.stanford.edu/wiki/images/math/8/5/a/85a1c5a07f21a9eebbfb1dca380f8d38.png) )。
)。
我們的目標是針對引數 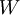 和
和 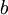 來求其函式
來求其函式 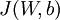 的最小值。為了求解神經網路,我們需要將每一個引數
的最小值。為了求解神經網路,我們需要將每一個引數 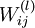
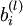 初始化為一個很小的、接近零的隨機值(比如說,使用正態分佈
初始化為一個很小的、接近零的隨機值(比如說,使用正態分佈 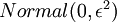 生成的隨機值,其中
生成的隨機值,其中 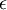 設定為
設定為 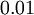 ),之後對目標函式使用諸如批量梯度下降法的最優化演算法。因為
),之後對目標函式使用諸如批量梯度下降法的最優化演算法。因為 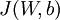 是一個非凸函式,梯度下降法很可能會收斂到區域性最優解;但是在實際應用中,梯度下降法通常能得到令人滿意的結果。最後,需要再次強調的是,要將引數進行隨機初始化,而不是全部置為
是一個非凸函式,梯度下降法很可能會收斂到區域性最優解;但是在實際應用中,梯度下降法通常能得到令人滿意的結果。最後,需要再次強調的是,要將引數進行隨機初始化,而不是全部置為 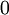 。如果所有引數都用相同的值作為初始值,那麼所有隱藏層單元最終會得到與輸入值有關的、相同的函式(也就是說,對於所有
。如果所有引數都用相同的值作為初始值,那麼所有隱藏層單元最終會得到與輸入值有關的、相同的函式(也就是說,對於所有  ,
,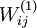 都會取相同的值,那麼對於任何輸入
都會取相同的值,那麼對於任何輸入  都會有:
都會有: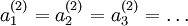 )。隨機初始化的目的是使對稱失效。
)。隨機初始化的目的是使對稱失效。
梯度下降法中每一次迭代都按照如下公式對引數 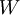 和
和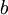 進行更新:
進行更新:
其中 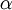 是學習速率。其中關鍵步驟是計算偏導數。我們現在來講一下反向傳播演算法,它是計算偏導數的一種有效方法。
是學習速率。其中關鍵步驟是計算偏導數。我們現在來講一下反向傳播演算法,它是計算偏導數的一種有效方法。
我們首先來講一下如何使用反向傳播演算法來計算 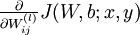 和
和 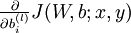 ,這兩項是單個樣例
,這兩項是單個樣例 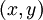 的代價函式
的代價函式 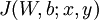 的偏導數。一旦我們求出該偏導數,就可以推匯出整體代價函式
的偏導數。一旦我們求出該偏導數,就可以推匯出整體代價函式 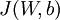 的偏導數:
的偏導數:
以上兩行公式稍有不同,第一行比第二行多出一項,是因為權重衰減是作用於 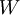 而不是
而不是 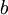 。
。
反向傳播演算法的思路如下:給定一個樣例 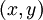 ,我們首先進行“前向傳導”運算,計算出網路中所有的啟用值,包括
,我們首先進行“前向傳導”運算,計算出網路中所有的啟用值,包括 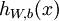 的輸出值。之後,針對第
的輸出值。之後,針對第  層的每一個節點
層的每一個節點  ,我們計算出其“殘差”
,我們計算出其“殘差” 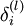 ,該殘差表明了該節點對最終輸出值的殘差產生了多少影響。對於最終的輸出節點,我們可以直接算出網路產生的啟用值與實際值之間的差距,我們將這個差距定義為
,該殘差表明了該節點對最終輸出值的殘差產生了多少影響。對於最終的輸出節點,我們可以直接算出網路產生的啟用值與實際值之間的差距,我們將這個差距定義為 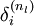 (第
(第 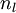 層表示輸出層)。對於隱藏單元我們如何處理呢?我們將基於節點(譯者注:第
層表示輸出層)。對於隱藏單元我們如何處理呢?我們將基於節點(譯者注:第  層節點)殘差的加權平均值計算
層節點)殘差的加權平均值計算 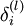 ,這些節點以
,這些節點以 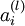 作為輸入。下面將給出反向傳導演算法的細節:
作為輸入。下面將給出反向傳導演算法的細節:
- 進行前饋傳導計算,利用前向傳導公式,得到
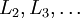 直到輸出層
直到輸出層 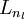 的啟用值。
的啟用值。 - 對於第
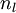 層(輸出層)的每個輸出單元
層(輸出層)的每個輸出單元  ,我們根據以下公式計算殘差:
,我們根據以下公式計算殘差:
-
- 對
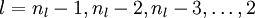 的各個層,第
的各個層,第  層的第
層的第  個節點的殘差計算方法如下:
個節點的殘差計算方法如下:
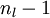 與
與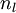 的關係替換為
的關係替換為 與
與 的關係,就可以得到:
的關係,就可以得到:
-
- 計算我們需要的偏導數,計算方法如下:
-
最後,我們用矩陣-向量表示法重寫以上演算法。我們使用“ ” 表示向量乘積運算子(在Matlab或Octave裡用“.*”表示,也稱作阿達馬乘積)。若
” 表示向量乘積運算子(在Matlab或Octave裡用“.*”表示,也稱作阿達馬乘積)。若 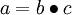 ,則
,則 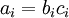 。在上一個教程中我們擴充套件了
。在上一個教程中我們擴充套件了 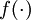 的定義,使其包含向量運算,這裡我們也對偏導數
的定義,使其包含向量運算,這裡我們也對偏導數 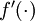 也做了同樣的處理(於是又有
也做了同樣的處理(於是又有 ![\textstyle f'([z_1, z_2, z_3]) = [f'(z_1), f'(z_2), f'(z_3)]](http://ufldl.stanford.edu/wiki/images/math/c/7/5/c7515c53b59e670ceee277e06c1229cb.png) )。
)。
那麼,反向傳播演算法可表示為以下幾個步驟:
- 進行前饋傳導計算,利用前向傳導公式,得到
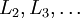 直到輸出層
直到輸出層 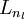 的啟用值。
的啟用值。 - 對輸出層(第
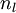 層),計算:
層),計算:
-
- 對於
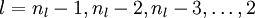 的各層,計算:
的各層,計算:
-
- 計算最終需要的偏導數值:
-
實現中應注意:在以上的第2步和第3步中,我們需要為每一個  值計算其
值計算其 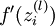 。假設
。假設 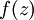 是sigmoid函式,並且我們已經在前向傳導運算中得到了
是sigmoid函式,並且我們已經在前向傳導運算中得到了 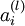 。那麼,使用我們早先推匯出的
。那麼,使用我們早先推匯出的 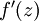 表示式,就可以計算得到
表示式,就可以計算得到 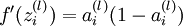 。
。
最後,我們將對梯度下降演算法做個全面總結。在下面的虛擬碼中,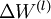 是一個與矩陣
是一個與矩陣 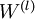 維度相同的矩陣,
維度相同的矩陣,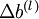 是一個與
是一個與 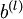 維度相同的向量。注意這裡“
維度相同的向量。注意這裡“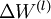 ”是一個矩陣,而不是“
”是一個矩陣,而不是“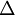 與
與 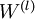 相乘”。下面,我們實現批量梯度下降法中的一次迭代:
相乘”。下面,我們實現批量梯度下降法中的一次迭代:
- 對於所有
 ,令
,令 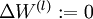 ,
, 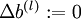 (設定為全零矩陣或全零向量)
(設定為全零矩陣或全零向量) - 對於
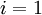 到
到 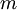 ,
,
- 使用反向傳播演算法計算
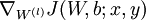 和
和 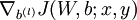 。
。 - 計算
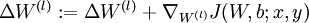 。
。 - 計算
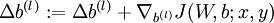 。
。
- 使用反向傳播演算法計算
- 更新權重引數:
-
現在,我們可以重複梯度下降法的迭代步驟來減小代價函式 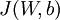 的值,進而求解我們的神經網路。
的值,進而求解我們的神經網路。

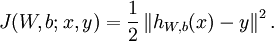
![\begin{align}J(W,b)&= \left[ \frac{1}{m} \sum_{i=1}^m J(W,b;x^{(i)},y^{(i)}) \right] + \frac{\lambda}{2} \sum_{l=1}^{n_l-1} \; \sum_{i=1}^{s_l} \; \sum_{j=1}^{s_{l+1}} \left( W^{(l)}_{ji} \right)^2 \\&= \left[ \frac{1}{m} \sum_{i=1}^m \left( \frac{1}{2} \left\| h_{W,b}(x^{(i)}) - y^{(i)} \right\|^2 \right) \right] + \frac{\lambda}{2} \sum_{l=1}^{n_l-1} \; \sum_{i=1}^{s_l} \; \sum_{j=1}^{s_{l+1}} \left( W^{(l)}_{ji} \right)^2\end{align}](http://ufldl.stanford.edu/wiki/images/math/4/5/3/4539f5f00edca977011089b902670513.png)
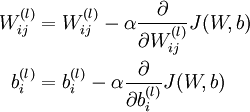
![\begin{align}\frac{\partial}{\partial W_{ij}^{(l)}} J(W,b) &=\left[ \frac{1}{m} \sum_{i=1}^m \frac{\partial}{\partial W_{ij}^{(l)}} J(W,b; x^{(i)}, y^{(i)}) \right] + \lambda W_{ij}^{(l)} \\\frac{\partial}{\partial b_{i}^{(l)}} J(W,b) &=\frac{1}{m}\sum_{i=1}^m \frac{\partial}{\partial b_{i}^{(l)}} J(W,b; x^{(i)}, y^{(i)})\end{align}](http://ufldl.stanford.edu/wiki/images/math/9/3/3/93367cceb154c392aa7f3e0f5684a495.png)
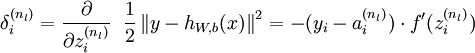
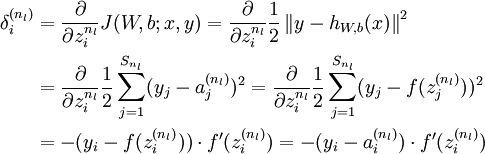
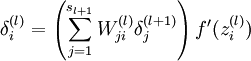
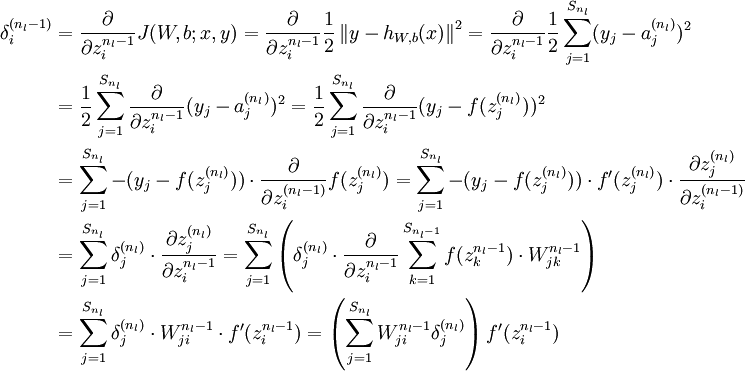
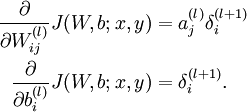
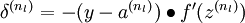
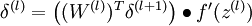
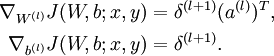
![\begin{align}W^{(l)} &= W^{(l)} - \alpha \left[ \left(\frac{1}{m} \Delta W^{(l)} \right) + \lambda W^{(l)}\right] \\b^{(l)} &= b^{(l)} - \alpha \left[\frac{1}{m} \Delta b^{(l)}\right]\end{align}](http://ufldl.stanford.edu/wiki/images/math/0/f/7/0f7430e97ec4df1bfc56357d1485405f.png)