深度學習基礎(七)—— Activation Function
阿新 • • 發佈:2019-01-06
1. Sigmoid
函式定義:
對應的影象是:
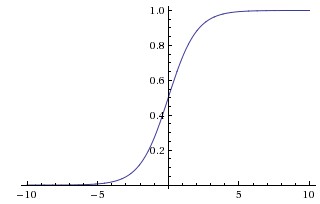
優點:
- Sigmoid函式的輸出對映在(0,1)之間,單調連續,輸出範圍有限,優化穩定,可以用作輸出層。
- 求導容易。
缺點:
- sigmoid容易飽和,出現梯度消失的現象。 sigmoid神經元的一個很差的屬性就是神經元的活躍度在0和1處飽和,它的梯度在這些地方接近於0。回憶在反向傳播中,某處的梯度和其目標輸出的梯度相乘,以得到整個目標。因此,如果某處的梯度過小,就會很大程度上出現梯度消失,使得幾乎沒有訊號經過這個神經元以及所有間接經過此處的資料。除此之外,人們必須額外注意sigmoid神經元權值的初始化來避免飽和。例如,當初始權值過大,幾乎所有的神經元都會飽和以至於網路幾乎不能學習。
- Sigmoid 的輸出不是0均值的,會導致後層的神經元的輸入是非0均值的訊號,這會對梯度產生影響:假設後層神經元的輸入都為正,那麼對w求區域性梯度則都為正,這樣在反向傳播的過程中w要麼都往正方向更新,要麼都往負方向更新,導致有一種捆綁的效果,使得收斂緩慢。 但是如果你是按batch去訓練,那麼每個batch可能得到不同的符號(正或負),那麼相加一下這個問題還是可以緩解。
2. Tanh
函式定義:
對應影象:

優點:
- 相比Sigmoid函式,其輸出以0為中心。
- 比Sigmoid函式收斂速度更快
缺點:
- 還是沒有改變Sigmoid函式的最大問題——由於飽和性產生的梯度消失。
3. ReLU
函式定義:
對應影象:
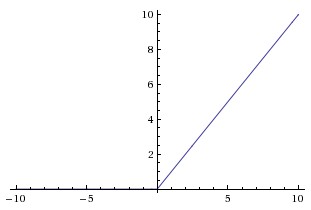
優點:
- 相比起Sigmoid和tanh,ReLU(e.g. a factor of 6 in Krizhevsky et al.)在SGD中能夠快速收斂。
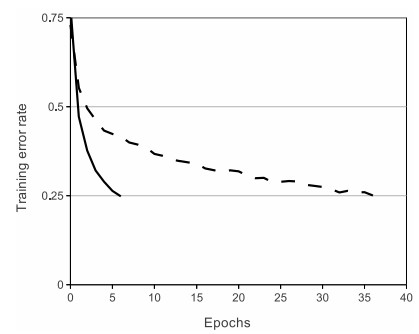
- Sigmoid和tanh涉及了很多很expensive的操作(比如指數),ReLU可以更加簡單的實現。
- 有效緩解了梯度消失的問題。
- 在無監督預訓練的時候也能有較好的表現。
- 提供了神經網路的稀疏表達能力。
缺點:
- 隨著訓練的進行,可能會出現神經元死亡,權重無法更新的情況。如果發生這種情況,那麼流經神經元的梯度從這一點開始將永遠是0。也就是說,ReLU神經元在訓練中不可逆地死亡了。例如,當學習速率設定過快時,60%的網路都“掛了”(神經元在此後的整個訓練中都不啟用)。當學習率設定恰當時,這種事情會更少出現。
4. LReLU、PReLU與RReLU
函式定義:
對應影象:
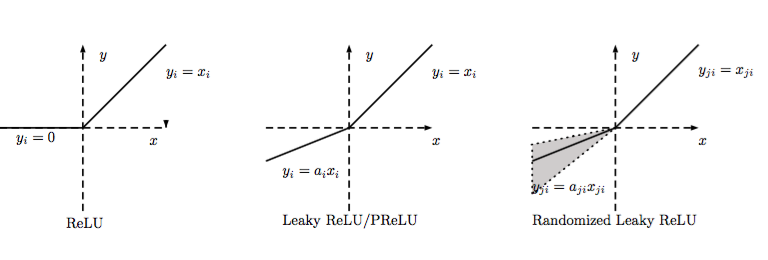
4.1 LReLU
當比較小而且固定的時候,我們稱之為LReLU。LReLU最初的目的是為了避免梯度消失。但在一些實驗中,我們發現LReLU對準確率並沒有太大的影響。很多時候,當應用LReLU時,必須要選取出合適的,LReLU的表現出的結果才比ReLU好。
4.2 PReLU
PReLU是LReLU的改進,可以自適應地從資料中學習引數。PReLU具有收斂速度快、錯誤率低的特點。PReLU可以用於反向傳播的訓練,可以與其他層同時優化。
- PReLU 只增加了極少量的引數,也就意味著網路的計算量以及過擬合的危險性都只增加了一點點。特別的,當不同channels使用相同的時,引數就更少了。
- BP更新時,採用的是帶動量的更新方式:
注意:上式的兩個係數分別是動量和學習率。 - 更新 時不施加權重衰減(L2正則化),因為這會把 很大程度上 push 到 0。事實上,即使不加正則化,試驗中 也很少有超過1的。
- 整個論文,被初始化為0.25。
- PReLU具有收斂速度快、錯誤率低的特點,可以用於反向傳播的訓練,可以與其他層同時優化。
4.3 RReLU
公式:
其中,是一個保持在給定範圍內取樣的隨機變數,在測試中是固定的。RReLU在一定程度上能起到正則效果。
4.4 ELU
公式:
