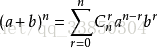基礎公式

先複習一下高中學的基礎知識
A(n, m) = n!/(n-m)! 從n個元素中有順序的取出m個元素。
C(n, m) = n!/((n-m)!m!) 從n個元素中無順序的取出m個元素。
高考選擇題中小技巧有排除法，分類討論法，插空法等。
二項式定理：

帕斯卡恆等式：
C(n + 1，r)=C(n + 1,r) = C(n,r - 1) + C(n,r);
因為(n + 1,r)是在n + 1個元素中選擇r個元素的無重複組合，那麼對於集合中的某個元素，要麼選，要麼不選，如果選的話就是C(n,r - 1)，如果不選就是C(n,r)。
它的用處主要是降低運算量，防止大數超時。

醒腦小例題

有n個人圍著桌子吃飯，請問有多少種排列方法？要是其中兩個人不想坐在一起呢？
解：（1）有n!/n種排列方法，因為圓桌需要指定一個開始坐的起點，n!則是沒有考慮起點問題，需要/n，或者認為隨機指定一個人先坐下，作為起點，剩下人再順一定方向坐。
（2）設a,b不想坐在一起，那考慮ab坐在一起的情況，相當於n-1個人在圍著桌子吃飯，其中a,b兩人可以ab或ba就坐，所以坐在一起的情況有2*(n-2)!，故此小問答案為(n-1)!-2*(n-2)!

遞推公式求通項

常見的有累加法，累乘法，構造法（設定引數法，拆分法，方程法構造出等差等比數列）
見此百度經驗，跟高中題目差不多

常見運算實現

• 求組合數C(n, r)
  公式看上去是比較簡單，但考慮到資料量大時可能會造成超時，需要用帕斯卡恆等式降低複雜度。但是層數過多遞迴也會造成大量重複計算，直接打個二維表更好。

int C[1010][1010] = {0};
void pre() {
    for (int i = 0; i < 1010; ++i) {
        C[i][0] = 1;
        for (int j = 1; j <= i; ++j) {
            C[i][j] = (C[i - 1][j] + C[i - 1][j - 1]) % MOD;
        }
 

    }
}

還看到一個比較trick的計算方式,仔細研究了求組合數的實際運算元素，分子上是大於a(max(r, n-r))的數，分母上是小於等於b(min(r, n-r))的數。

long long int C1(int n, int r){
	int a, b;
	long long int res=1;
	a = r>(n-r)?r:n-r;
	b = n - a;
	for (int i=n; i>0; i--){
		if(i > a) res *= i;
		else if (i <= b) res /= i;
	}
	return res;
}

• 快速冪求模
  排列組合中常見a^b中a和b都是大數，一般需要的就是一邊求冪，一邊取餘。
  基本操作：

//p^q mod m
for (int i=0; i<q; i++) res = (res * p)%m;

快速冪求模中要想辦法降低a和b的規模，根據引理：積的取餘等於取餘的積的取餘。首先我們可以a%=m 來降低a的大小，再通過合併a*a降低b的大小。程式碼實現：

long long Mode(long long a, long long b, long long mode)
{
	long long sum = 1;//最終結果
	while (b) {
		if (b & 1) {//位運算判斷奇偶性
			sum = (sum * a) % mode;//是奇數的話先乘以下a
		}
		b /= 2;//降低了b的大小
		a = a * a % mode;//合併a*a,再mod一下
	}
	return sum;
}