全文轉自：https://www.cnblogs.com/gatherstars/p/6084696.html#commentform

這篇真的講的清楚明白！要多複習！加深記憶！

1.概述

　　AUC（Area Under roc Curve）是一種用來度量 分類模型好壞的一個標準。這樣的標準其實有很多，例如：大約10年前在machine learning文獻中一統天下的標準：分類精度；在資訊檢索(IR)領域中常用的recall和 precision，等等。其實，度量反應了人們對”好”的分類結果的追求，同一時期的不同的度量反映了人們對什麼是”好”這個最根本問題的不同認識，而不同時期流行的度量則反映了人們認識事物的深度的變化。 　　近年來，隨著machine learning的相關技術從實驗室走向實際應用，一些實際的問題對度量標準提出了新的需求。特別的，現實中樣本在不同類別上的不均衡分佈(class distribution imbalance problem)。使得accuracy這樣的傳統的度量標準不能恰當的反應分類器的performance。舉個例子：測試樣本中有A類樣本90個，B 類樣本10個。分類器C1把所有的測試樣本都分成了A類，分類器C2把A類的90個樣本分對了70個，B類的10個樣本分對了5個。則C1的分類精度為 90%，C2的分類精度為75%。但是，顯然C2更有用些。另外，在一些分類問題中犯不同的錯誤代價是不同的(cost sensitive learning)。這樣，預設0.5為分類閾值的傳統做法也顯得不恰當了。 為了解決上述問題，人們從醫療分析領域引入了一種新的分類模型 performance評判方法——ROC分析。ROC分析本身就是一個很豐富的內容，有興趣的讀者可以自行Google，這裡只做些簡單的概念性的介紹。 　　ROC的全名叫做Receiver Operating Characteristic，其主要分析工具是一個畫在二維平面上的曲線——ROC curve。平面的橫座標是false positive rate(FPR)，縱座標是true positive rate(TPR)。對某個分類器而言，我們可以根據其在測試樣本上的表現得到一個TPR和FPR點對。這樣，此分類器就可以對映成ROC平面上的一個點。調整這個分類器分類時候使用的閾值，我們就可以得到一個經過(0, 0)，(1, 1)的曲線，這就是此分類器的ROC曲線。一般情況下，這個曲線都應該處於(0, 0)和(1, 1)連線的上方。因為(0, 0)和(1, 1)連線形成的ROC曲線實際上代表的是一個隨機分類器。如果很不幸，你得到一個位於此直線下方的分類器的話，一個直觀的補救辦法就是把所有的預測結果反向，即：分類器輸出結果為正類，則最終分類的結果為負類，反之，則為正類。雖然，用ROC curve來表示分類器的performance很直觀好用。可是，人們總是希望能有一個數值來標誌分類器的好壞。於是Area Under roc Curve(AUC)就出現了。顧名思義，AUC的值就是處於ROC curve下方的那部分面積的大小。通常，AUC的值介於0.5到1.0之間，較大的AUC代表了較好的performance。

2.ROC曲線

2.1ROC的動機

　　對於0，1兩類分類問題，一些分類器得到的結果往往不是0，1這樣的標籤，如神經網路得到諸如0.5，0.8這樣的分類結果。這時，我們人為取一個閾值，比如0.4，那麼小於0.4的歸為0類，大於等於0.4的歸為1類，可以得到一個分類結果。同樣，這個閾值我們可以取0.1或0.2等等。取不同的閾值，最後得到的分類情況也就不同。如下面這幅圖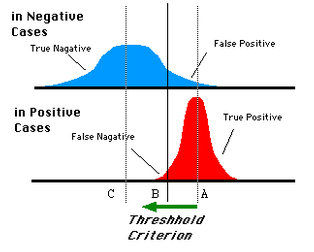： 　　藍色表示原始為負類分類得到的統計圖，紅色表示原始為正類得到的統計圖。那麼我們取一條直線，直線左邊分為負類，直線右邊分為正類，這條直線也就是我們所取的閾值。閾值不同，可以得到不同的結果，但是由分類器決定的統計圖始終是不變的。這時候就需要一個獨立於閾值，只與分類器有關的評價指標，來衡量特定分類器的好壞。還有在類不平衡的情況下，如正樣本有90個，負樣本有10個，直接把所有樣本分類為正樣本，得到識別率為90%，但這顯然是沒有意義的。如上就是ROC曲線的動機。

2.2ROC的定義

　　關於兩類分類問題，原始類為positive、negative，分類後的類別為p'、n'。排列組合後得到4種結果，如下圖所示：   　　於是我們得到四個指標，分別為：真陽、偽陽、偽陰、真陰。ROC空間將偽陽性率（FPR）定義為 X 軸，真陽性率（TPR）定義為 Y 軸。這兩個值由上面四個值計算得到，公式如下： 　　TPR：在所有實際為陽性的樣本中，被正確地判斷為陽性之比率。TPR=TP/(TP+FN) 　　FPR：在所有實際為陰性的樣本中，被錯誤地判斷為陽性之比率。FPR=FP/(FP+TN) 　　放在具體領域來理解上述兩個指標。如在醫學診斷中，判斷有病的樣本。那麼儘量把有病的揪出來是主要任務，也就是第一個指標TPR，要越高越好。而把沒病的樣本誤診為有病的，也就是第二個指標FPR，要越低越好。不難發現，這兩個指標之間是相互制約的。如果某個醫生對於有病的症狀比較敏感，稍微的小症狀都判斷為有病，那麼他的第一個指標應該會很高，但是第二個指標也就相應地變高。最極端的情況下，他把所有的樣本都看做有病，那麼第一個指標達到1，第二個指標也為1。

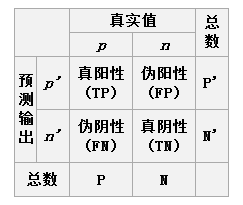
2.3ROC的圖形化表示

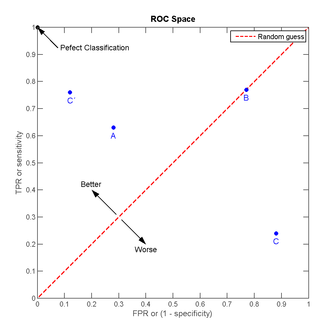
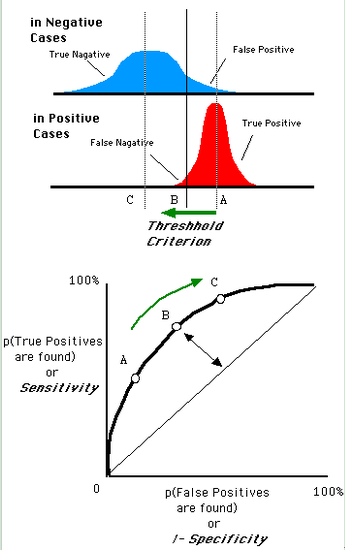
　　我們以FPR為橫軸，TPR為縱軸，得到如下ROC空間： 　　我們可以看出：左上角的點（TPR=1，FPR=0），為完美分類，也就是這個醫生醫術高明，診斷全對；點A（TPR>FPR），醫生A的判斷大體是正確的。中線上的點B（TPR=FPR），也就是醫生B全都是蒙的，蒙對一半，蒙錯一半；下半平面的點C（TPR<FPR），這個醫生說你有病，那麼你很可能沒有病，醫生C的話我們要反著聽，為真庸醫。 上圖中一個閾值，得到一個點。現在我們需要一個獨立於閾值的評價指標來衡量這個醫生的醫術如何，也就是遍歷所有的閾值，得到ROC曲線。還是一開始的那幅圖，假設如下就是某個醫生的診斷統計圖，直線代表閾值。我們遍歷所有的閾值，能夠在ROC平面上得到如下的ROC曲線。

　　曲線距離左上角越近，證明分類器效果越好。

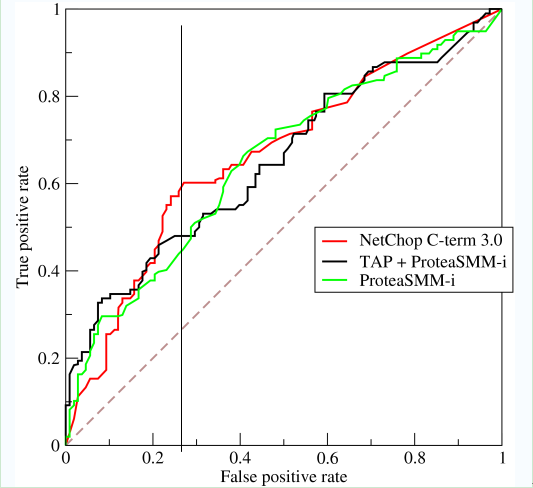　　如上，是三條ROC曲線，在0.23處取一條直線。那麼，在同樣的FPR=0.23的情況下，紅色分類器得到更高的TPR。也就表明，ROC越往上，分類器效果越好。我們用一個標量值AUC來量化他。

3.AUC值

3.1AUC值的定義

　　AUC值為ROC曲線所覆蓋的區域面積，顯然，AUC越大，分類器分類效果越好。 　　AUC = 1，是完美分類器，採用這個預測模型時，不管設定什麼閾值都能得出完美預測。絕大多數預測的場合，不存在完美分類器。 　　0.5 < AUC < 1，優於隨機猜測。這個分類器（模型）妥善設定閾值的話，能有預測價值。 　　AUC = 0.5，跟隨機猜測一樣（例：丟銅板），模型沒有預測價值。 　　AUC < 0.5，比隨機猜測還差；但只要總是反預測而行，就優於隨機猜測。

3.2AUC值的物理意義

　　假設分類器的輸出是樣本屬於正類的socre（置信度），則AUC的物理意義為，任取一對（正、負）樣本，正樣本的score大於負樣本的score的概率。

3.3AUC值的計算

　　（1）第一種方法：AUC為ROC曲線下的面積，那我們直接計算面積可得。面積為一個個小的梯形面積之和，計算的精度與閾值的精度有關。 　　（2）第二種方法：根據AUC的物理意義，我們計算正樣本score大於負樣本的score的概率。取N*M（N為正樣本數，M為負樣本數）個二元組，比較score，最後得到AUC。時間複雜度為O(N*M)。 　　（3）第三種方法：與第二種方法相似，直接計算正樣本score大於負樣本的score的概率。我們首先把所有樣本按照score排序，依次用rank表示他們，如最大score的樣本，rank=n(n=N+M)，其次為n-1。那麼對於正樣本中rank最大的樣本（rank_max），有M-1個其他正樣本比他score小，那麼就有(rank_max-1)-(M-1)個負樣本比他score小。其次為(rank_second-1)-(M-2)。最後我們得到正樣本大於負樣本的概率為： 時間複雜度為O(N+M)。