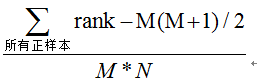ROC曲線與AUC
ROC曲線
對於0,1兩類分類問題,一些分類器得到的結果往往不是0,1這樣的標籤,如神經網路,得到諸如0.5,0,8這樣的分類結果。這時,我們人為取一個閾值,比如0.4,那麼小於0.4的為0類,大於等於0.4的為1類,可以得到一個分類結果。同樣,這個閾值我們可以取0.1,0.2等等。取不同的閾值,得到的最後的分類情況也就不同。
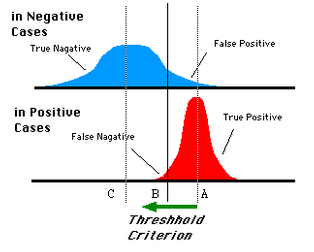
如下面這幅圖:
藍色表示原始為負類分類得到的統計圖,紅色為正類得到的統計圖。那麼我們取一條直線,直線左邊分為負類,右邊分為正,這條直線也就是我們所取的閾值。
閾值不同,可以得到不同的結果,但是由分類器決定的統計圖始終是不變的。這時候就需要一個獨立於閾值,只與分類器有關的評價指標,來衡量特定分類器的好壞。
還有在類不平衡的情況下,如正樣本90個,負樣本10個,直接把所有樣本分類為正樣本,得到識別率為90%。但這顯然是沒有意義的。
如上就是ROC曲線的動機。
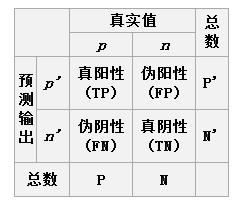
關於兩類分類問題,原始類為positive,negative,分類後的類別為p,n。排列組合後得到4種結果,如下:
於是我們得到四個指標,分別為真陽,偽陽;偽陰,真陰。
ROC空間將偽陽性率(FPR)定義為 X 軸,真陽性率(TPR)定義為 Y 軸。這兩個值由上面四個值計算得到,公式如下:
TPR:在所有實際為陽性的樣本中,被正確地判斷為陽性之比率。
TPR=TP/(TP+FN)
FPR:在所有實際為陰性的樣本中,被錯誤地判斷為陽性之比率。
FPR=FP/(FP+TN)
放在具體領域來理解上述兩個指標。
如在醫學診斷中,判斷有病的樣本。
那麼儘量把有病的揪出來是主要任務,也就是第一個指標TPR,要越高越好。
而把沒病的樣本誤診為有病的,也就是第二個指標FPR,要越低越好。
不難發現,這兩個指標之間是相互制約的。如果某個醫生對於有病的症狀比較敏感,稍微的小症狀都判斷為有病,那麼他的第一個指標應該會很高,但是第二個指標也就相應地變高。最極端的情況下,他把所有的樣本都看做有病,那麼第一個指標達到1,第二個指標也為1。
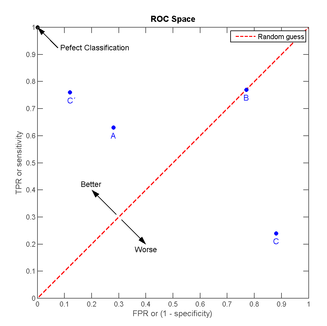
我們以FPR為橫軸,TPR為縱軸,得到如下ROC空間。
我們可以看出,左上角的點(TPR=1,FPR=0),為完美分類,也就是這個醫生醫術高明,診斷全對。
點A(TPR>FPR),醫生A的判斷大體是正確的。中線上的點B(TPR=FPR),也就是醫生B全都是蒙的,蒙對一半,蒙錯一半;下半平面的點C(TPR<FPR),這個醫生說你有病,那麼你很可能沒有病,醫生C的話我們要反著聽,為真庸醫。
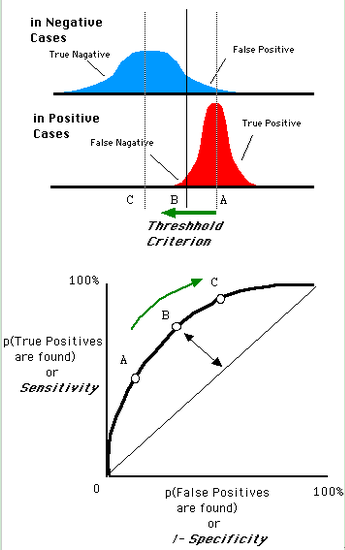
上圖中一個閾值,得到一個點。現在我們需要一個獨立於閾值的評價指標來衡量這個醫生的醫術如何,也就是遍歷所有的閾值,得到ROC曲線。
還是一開始的那幅圖,假設如下就是某個醫生的診斷統計圖,直線代表閾值。我們遍歷所有的閾值,能夠在ROC平面上得到如下的ROC曲線。
曲線距離左上角越近,證明分類器效果越好。
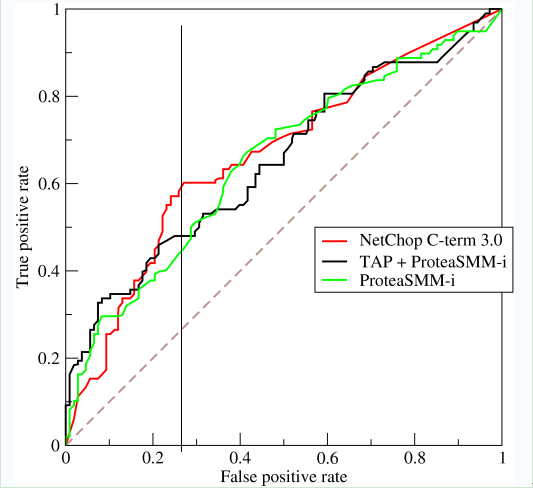
如上,是三條ROC曲線,在0.23處取一條直線。那麼,在同樣的低FPR=0.23的情況下,紅色分類器得到更高的PTR。也就表明,ROC越往上,分類器效果越好。我們用一個標量值AUC來量化他。
AUC
AUC值為ROC曲線所覆蓋的區域面積,顯然,AUC越大,分類器分類效果越好。
AUC = 1,是完美分類器,採用這個預測模型時,不管設定什麼閾值都能得出完美預測。絕大多數預測的場合,不存在完美分類器。
0.5 < AUC < 1,優於隨機猜測。這個分類器(模型)妥善設定閾值的話,能有預測價值。
AUC = 0.5,跟隨機猜測一樣(例:丟銅板),模型沒有預測價值。
AUC < 0.5,比隨機猜測還差;但只要總是反預測而行,就優於隨機猜測。
AUC的物理意義
假設分類器的輸出是樣本屬於正類的socre(置信度),則AUC的物理意義為,任取一對(正、負)樣本,正樣本的score大於負樣本的score的概率。
計算AUC:
第一種方法:AUC為ROC曲線下的面積,那我們直接計算面積可得。面積為一個個小的梯形面積之和。計算的精度與閾值的精度有關。
第二種方法:根據AUC的物理意義,我們計算正樣本score大於負樣本的score的概率。取N*M(N為正樣本數,M為負樣本數)個二元組,比較score,最後得到AUC。時間複雜度為O(N*M)。
第三種方法:與第二種方法相似,直接計算正樣本score大於負樣本的概率。我們首先把所有樣本按照score排序,依次用rank表示他們,如最大score的樣本,rank=n(n=N+M),其次為n-1。那麼對於正樣本中rank最大的樣本,rank_max,有M-1個其他正樣本比他score小,那麼就有(rank_max-1)-(M-1)個負樣本比他score小。其次為(rank_second-1)-(M-2)。最後我們得到正樣本大於負樣本的概率為
時間複雜度為O(N+M)。
MATLAB實現
MATLAB自帶plotroc()方法,繪製ROC曲線,引數如下:
plotroc(targets,outputs);
第一個引數為測試樣本的原始標籤,第二個引數為分類後得到的標籤。
兩個為行或列向量,相同維數即可。
AUC matlab程式碼:
function [result]=AUC(test_targets,output)
%計算AUC值,test_targets為原始樣本標籤,output為分類器得到的標籤
%均為行或列向量
[A,I]=sort(output);
M=0;N=0;
for i=1:length(output)
if(test_targets(i)==1)
M=M+1;
else
N=N+1;
end
end
sigma=0;
for i=M+N:-1:1
if(test_targets(I(i))==1)
sigma=sigma+i;
end
end
result=(sigma-(M+1)*M/2)/(M*N);相關推薦
ROC曲線與AUC區域的理解與實踐
Receiver Operating Characteristic Area Under the Curve (ROC and AUC). 如何向別人解釋 ROC AUC 對評價機器學習演算法的意義: 一個樣本集,一半正樣本,一半為負樣本。如果一個機器
ROC曲線與AUC--模型評價指標
ROC(Receiver Operating Characteristic) 主要分析工具是一個畫在二維平面上的曲線——ROC curve。 平面的橫座標是 false positive rate(FPR),縱座標是 true positive rate(TPR)。 相關概念 True Positive R
ROC曲線與AUC以及LIFT
ROC曲線 對於0,1兩類分類問題,一些分類器得到的結果往往不是0,1這樣的標籤,如神經網路,得到諸如0.5,0,8這樣的分類結果。這時,我們人為取一個閾值,比如0.4,那麼小於0.4的為0類,大於等於0.4的為1類,可以得到一個分類結果。同樣,這個閾值我們可以取0.1,0.2等等。取不同的閾值,得到的最
模型評估與選擇(中篇)-ROC曲線與AUC曲線
P-R曲線 以二分類問題為例進行說明。分類結果的混淆矩陣如下圖所示。 假設,現在我們用某一演算法h對樣本進行二分類(劃分為正例、反例)。由於演算法可能與理想方法存在誤差,因此在劃分結果中,劃分為正例的那部分樣本中,可能存在正例,也可能存在反例。同理,
ROC曲線與AUC
ROC曲線 對於0,1兩類分類問題,一些分類器得到的結果往往不是0,1這樣的標籤,如神經網路,得到諸如0.5,0,8這樣的分類結果。這時,我們人為取一個閾值,比如0.4,那麼小於0.4的為0類,大於等於0.4的為1類,可以得到一個分類結果。同樣,這個閾值我們可以取0.1,
ROC曲線與AUC計算
ROC曲線繪製與AUC計算 宣告: 1)該博文是整理自網上很大牛和專家所無私奉獻的資料的。具體引用的資料請看參考文獻。具體的版本宣告也參考原文獻2)本文僅供學術交流,非商用。所以每一部分具體的參考資料並沒有詳細對應,更有些部分本來就是直接從其他部落格複製過來的。如果某部分不
統計分析之ROC曲線與多指標聯合分析——附SPSS繪製ROC曲線指南
在進行某診斷方法的評估是,我們常常要用到ROC曲線。這篇博文將簡要介紹ROC曲線以及用SPSS及medcal繪製ROC曲線的方法。 定義 ROC受試者工作特徵曲線 (receive
從roc曲線到auc
1.為什麼我們要用roc曲線進行評價 用傳統的識別率來評價模型的話會有下面的缺陷: 在類不平衡的情況下, 如正樣本90個,負樣本10個,直接把所有樣本分類為正樣本,得到識別率為90% 而如果正樣本識別對75個,負樣本識別對5個,得到的識別率為80%。 但是這樣的識別率評價指標導致高分
ROC曲線及AUC
ROC曲線 意義 ROC曲線指受試者工作特徵曲線 / 接收器操作特性曲線(receiver operating characteristic curve),是反映敏感性和特異性連續變數的綜合指標,是用構圖法揭示敏感性和特異性的相互關係,它通過將連續變數設定出多個不同的臨界值,從而計算出一系列
【深度學習-機器學習】分類度量指標 : 正確率、召回率、靈敏度、特異度,ROC曲線、AUC等
在分類任務中,人們總是喜歡基於錯誤率來衡量分類器任務的成功程度。錯誤率指的是在所有測試樣例中錯分的樣例比例。實際上,這樣的度量錯誤掩蓋了樣例如何被分錯的事實。在機器學習中,有一個普遍適用的稱為混淆矩陣(confusion matrix)的工具,它可以幫助人們更好地瞭解
機器學習中模型的效能度量方式:混淆矩陣,F1-Score、ROC曲線、AUC曲線。
一、混淆矩陣 混淆矩陣也稱誤差矩陣,是表示精度評價的一種標準格式,混淆矩陣的每一列代表了預測類別,每一列的總數表示預測為該類別的資料的數目;每一行代表了資料的真實歸屬類別 ,每一行的資料總數表示該類別的資料例項的數目。每一列中的數值表示真實資料被預測為該類的數目。
分類模型的評價指標--混淆矩陣,F1-score,ROC曲線,AUC,KS曲線
1. 混淆矩陣---確定截斷點後,評價學習器效能 TP(實際為正預測為正),FP(實際為負但預測為正),FN(實際為正但預測為負),TN(實際為負預測為負) 通過混淆矩陣我們可以給出各指標的值: 查全率(召回率,Recall):樣本中的正例有多少被預測準確了,衡量的
機器學習評估指標:Precision、recall、F-measure、Accuracy、ROC曲線和AUC
在使用機器學習演算法的過程中,我們需要對建立的模型進行評估來辨別模型的優劣,下文中主要介紹我在學習中經常遇見的幾種評估指標。以下指標都是對分類問題的評估指標。 將標有正負例的資料集餵給模型後,一般能夠得到下面四種情況: True Positive(TP),模型
ROC曲線和AUC
本博文所有理論都是基於二分類,多分類問題其實與二分類問題想通。 1,首先區分什麼是正類什麼是負類。 考慮一個二分問題,如果一類定為正類(positive),那麼另一類就是負類(negative)。 注意和正樣本和負樣本概念不同,參考博文:https://blog.c
幾個易混淆的概念(準確率-召回率,擊中率-虛警率,PR曲線和mAP,ROC曲線和AUC)
準確率、召回率、F1 資訊檢索、分類、識別、翻譯等領域兩個最基本指標是召回率(Recall Rate)和準確率(Precision Rate),召回率也叫查全率,準確率也叫查準率,概念公式: 召回率(Recall) = 系統檢索到的相關檔案 / 系統所有相關的檔
分類器評價指標--ROC曲線及AUC值
ROC和AUC介紹以及如何計算AUC ROC(Receiver Operating Characteristic)曲線和AUC常被用來評價一個二值分類器(binary classifier)的優劣,對兩者的簡單介紹見這裡。這篇博文簡單介紹ROC和AUC的特點,以及更為深
ROC曲線的AUC(以及其他評價指標的簡介)知識整理
相關評價指標在這片文章裡有很好介紹 ROC曲線:接收者操作特徵(receiveroperating characteristic) 比較分類模型的可視工具,曲線上各點反映著對同一訊號刺激的感受性。 縱軸:真正率(擊中率)true positive rate ,TPR,
精確率(準確率、查準率、precision)、召回率(查全率、recall)、RoC曲線、AUC面積、PR曲線
精確率(Precision)的定義如下: P=TPTP+FP 召回率(Recall)的定義如下: R=TPTP+FN 特異性(specificity)的定義如下: S=FPFP+TN 有時也用一個F1值來綜合評估精確率和召回率,它是精確率和召回
ROC曲線及AUC評價指標
一,簡介 對訓練出的分類器的分類效果的評估,常見有精確度(accuracy),PR(precision- recall), precision等,一般來說訓練樣本數量越大,則的儲的 用的就是分類器的精確度(accuracy),在某些如推薦或資訊獲取領域還會組合使用pr
精確率與召回率,RoC曲線與PR曲線
在機器學習的演算法評估中,尤其是分類演算法評估中,我們經常聽到精確率(precision)與召回率(recall),RoC曲線與PR曲線這些概念,那這些概念到底有什麼用處呢? 首先,我們需要搞清楚幾個拗口的概念: 1. TP, FP, TN, F